Advertisements
Advertisements
Question
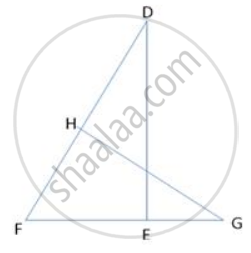
Observe the figure and complete the following activity
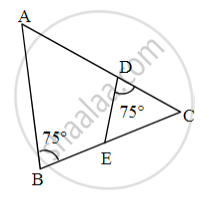
In fig, ∠B = 75°, ∠D = 75°
∠B ≅ [ ______ ] ...[each of 75°]
∠C ≅ ∠C ...[ ______ ]
ΔABC ~ Δ [ ______ ] ...[ ______ similarity test]
Solution
In fig, ∠B = 75°, ∠D = 75°
∠B ≅ ∠D ...[each of 75°]
∠C ≅ ∠C ...[Common angle]
ΔABC ~ ΔEDC ...[AA similarity test]]
APPEARS IN
RELATED QUESTIONS
In figure, considering triangles BEP and CPD, prove that BP × PD = EP × PC.
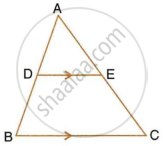
In the following figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

Given: ∠GHE = ∠DFE = 90°,
DH = 8, DF = 12,
DG = 3x – 1 and DE = 4x + 2.
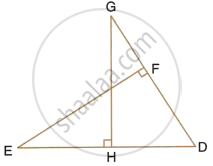
Find: the lengths of segments DG and DE.
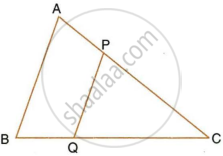
In the figure, PQRS is a parallelogram with PQ = 16 cm and QR = 10 cm. L is a point on PR such that RL : LP = 2 : 3. QL produced meets RS at M and PS produced at N.

Find the lengths of PN and RM.
The given figure shows a triangle PQR in which XY is parallel to QR. If PX : XQ = 1 : 3 and QR = 9 cm, find the length of XY.
Further, if the area of ΔPXY = x cm2; find, in terms of x the area of :
- triangle PQR.
- trapezium XQRY.
Δ ABC ~ Δ DEF. If BC = 3cm , EF=4cm and area of Δ ABC = 54 cm2 , find area of Δ DEF.
In figure , DEF is a right -angled triangle with ∠ E = 90 °.FE is produced to G and GH is drawn perpendicular to DE = 8 cm , DH = 8 cm ,DH = 6 cm and HF = 4 cm , find `("Ar" triangle "DEF")/("Ar" triangle "GHF")`
A model of a ship is made with a scale factor of 1 : 500. Find
The length of the ship, if the model length is 60 cm.
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The area in km2 that can be represented by 1 cm2
In the following figure, point D divides AB in the ratio 3 : 5. Find :
- `(AE)/(EC)`
- `(AD)/(AB)`
- `(AE)/(AC)`
Also, if: - DE = 2.4 cm, find the length of BC.
- BC = 4.8 cm, find the length of DE.
In the given figure, PQ || AB; CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm. Find :
- `(CP)/(PA)`
- PQ
- If AP = x, then the value of AC in terms of x.
Construct a ΔABC in which CA = 6 cm, AB = 5 cm and ∠BAC = 45°. Then construct a triangle whose sides are `3/5` of the corresponding sides of ΔABC.
In ΔABC, MN is drawn parallel to BC. If AB = 3.5cm, AM : AB = 5 : 7 and NC = 2cm, find:
(i) AM
(ii) AC
ΔABC has been reduced by a scale factor 0.6 to ΔA'B'C'/ Calculate:Length of B' C', if BC = 8cm
ΔABC is enlarged, with a scale factor 5. Find: A'B', if AB = 4cm
The scale of a map is 1 : 50000. The area of a city is 40 sq km which is to be represented on the map. Find: The area of land represented on the map.
If ∆ABC ~ ∆DEF such that area of ∆ABC is 9 cm2 and the area of ∆DEF is 16 cm2 and BC = 2.1 cm. Find the length of EF.
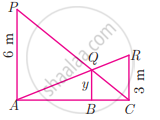
Two vertical poles of heights 6 m and 3 m are erected above a horizontal ground AC. Find the value of y
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that b2 + c2 = `2"p"^2 + "a"^2/2`
In ΔABC, PQ || BC. If PB = 6 cm, AP = 4 cm, AQ = 8 cm, find the length of AC.