Advertisements
Advertisements
Question
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that b2 + c2 = `2"p"^2 + "a"^2/2`
Solution
Given ∠AED = 90°
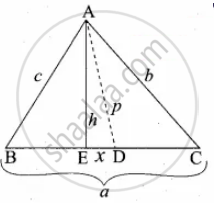
ED = x, DC = `"a"/2` ...(D is the mid point of BC)
∴ EC = `x + "a"/2`, BE = `"a"/2 - x`
∴ In the right ∆AED
AD2 = AE2 + ED2
p2 = h2 + x2
In the right ∆AEC,
AC2 = AE2 + EC2
b2 = `"h"^2 + (x + "a"/2)^2`
= `"h"^2 + x^2 + "a"^2/4 + 2 xx x xx "a"/2`
b2 = `"p"^2 + "a"^2/4 + "a"x` ......(1)
b2 = `"p"^2 + "a"x + 1/4 "a"^2` ....(2)
In the right triangle ABE,
AB2 = AE2 + BE2
c2 = h2 + (a2 – x)2
c2 = h2 + a24 + x2 – ax
c2 = h2 + x2 + 14 a2 – ax
c2 = p2 – ax + `a^2/4` .....(3)
By adding (2) and (3)
b2 + c2 = `"p"^2 + "a"x + "a"^2/4 + "p"^2 - "a"x + "a"^2/4`
= `2"p"^2 + (2"a"^2)/4`
= `2"p"^2 + "a"^2/2`
APPEARS IN
RELATED QUESTIONS
In a triangle ABC, line l || Side BC and line l intersects side AB and AC in points P and Q, respectively. Prove that: `"AP"/"BP"="AQ"/"QC"`

A model of a ship if made to a scale of 1 : 200.
(i) Thelength of the model is 4 m; calculate the length of the ship.
(ii) The area of the deck of the ship is 160000 m2; find the area of the deck of the model.
(iii) The volume of the model is 200 litres; calculate the volume of the ship in m3.
The perimeter of two similar triangles ABC and PQR are 32cm and 24cm respectively. If PQ = 12cm, find AB.
In the following figure, seg BE ⊥ seg AB and seg BA ⊥ seg AD. If BE = 6 and \[\text{AD} = 9 \text{ find} \frac{A\left( \Delta ABE \right)}{A\left( \Delta BAD \right)} \cdot\]

A model of a ship is made with a scale factor of 1 : 500. Find
The deck area of the model, if the deck area of the ship is 1500000 m2
Find the scale factor in each of the following and state the type of size transformation:
Actual length = 12cm, Image length = 15cm.
In the adjacent figure, ∆ACB ~ ∆APQ. If BC = 8 cm, PQ = 4 cm, BA = 6.5 cm and AP = 2.8 cm, find CA and AQ

If BD ⊥ AC and CE ⊥ AB, prove that ∆AEC ~ ∆ADB

An architecture have model of building. Length of building is 1 m then length of model is 0.75 cm. Then find length and height of model building whose actual length is 22.5 m and height is 10 m
In ∠BAC = 90° and AD ⊥ BC. A then ______.

