Advertisements
Advertisements
Question
The perimeter of two similar triangles ABC and PQR are 32cm and 24cm respectively. If PQ = 12cm, find AB.
Solution
It is given that triangles ABC and PQR are similar. Therefore,
`("permeter (ΔABC)")/("PErimeter (ΔPQR)")=(AB)/(PQ)`
⇒` 32/24=(AB)/12`
⇒` AB=(32xx12)/24=16 cm`
APPEARS IN
RELATED QUESTIONS
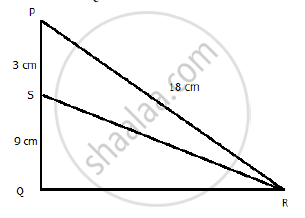
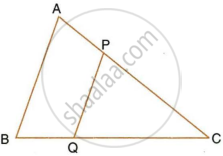
In the following figure, in Δ PQR, seg RS is the bisector of ∠PRQ.
PS = 3, SQ = 9, PR = 18. Find QR.
In ∆ABC, DE is parallel to base BC, with D on AB and E on AC. If `\frac{AD}{DB}=\frac{2}{3}` , find `\frac{BC}{DE}.`
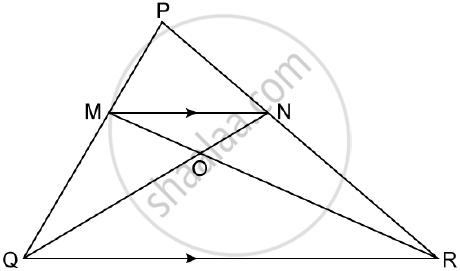
In ΔPQR, MN is parallel to QR and `(PM)/(MQ) = 2/3`
1) Find `(MN)/(QR)`
2) Prove that ΔOMN and ΔORQ are similar.
3) Find, Area of ΔOMN : Area of ΔORQ
In the given figure, AB || EF || DC; AB = 67.5 cm, DC = 40.5 cm and AE = 52.5 cm.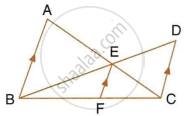
- Name the three pairs of similar triangles.
- Find the lengths of EC and EF.
Two chords AB and CD of a circle intersect at a point P outside the circle.
Prove that: (i) Δ PAC ~ Δ PDB (ii) PA. PB = PC.PD

The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5cm, find the length of QR.
In the figure, parts of the two triangles bearing identical marks are
congruent. State the test by which the triangles are congruent.
If Δ ABC , MN || BC .
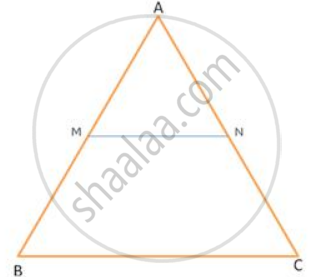
If AN : AC= 5 : 8, find ar(Δ AMN) : ar(Δ ABC)
In Δ PQR, MN is drawn parallel to QR. If PM = x, MQ = (x-2), PN = (x+2) and NR = (x-1), find the value of x.
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The number of kilometres on the ground represented by lcm or the map
A triangle ABC has been enlarged by scale factor m = 2.5 to the triangle A' B' C'. Calculate : the length of AB, if A' B' = 6 cm.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : OA, if OA' = 6 cm.
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and ∠ABC = 90°.
Calculate : the actual lengths of AB and BC in km.
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and angle ABC = 90°.
Calculate : the area of the plot in sq. km.
In the following figure, point D divides AB in the ratio 3 : 5. Find : `(AD)/(AB)`
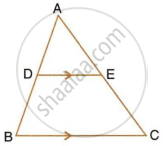
In the given figure, PQ || AB; CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm. Find :
- `(CP)/(PA)`
- PQ
- If AP = x, then the value of AC in terms of x.
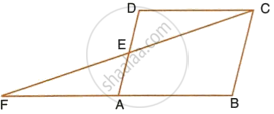
The given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.
Let ∆ ABC ∽ ∆ DEF and their areas be respectively, 64 cm2 and 121 cm2. If EF = 15⋅4 cm, find BC.
In ΔPQR, L and M are two points on the base QR, such that ∠LPQ = ∠QRP and ∠RPM = ∠RQP.
Prove that : (i) ΔPQL ∼ ΔRPM
(ii) QL. Rm = PL. PM
(iii) PQ2 = QR. QL.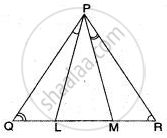
In the given figure, ABC is a triangle. DE is parallel to BC and `"AD"/"DB" = (3)/(2)`.
(i) Determine the ratios `"AD"/"AB","DE"/"BC"`.
(ii) Prove that ΔDEF is similar to ΔCBF.
Hence, find `"EF"/"FB"`.
(iii) What is the ratio of the areas of ΔDEF and ΔBFC?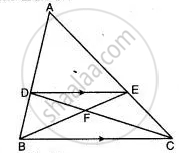
In the given figure ABC and CEF are two triangles where BA is parallel to CE and AF: AC = 5: 8.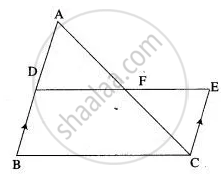
(i) Prove that ΔADF ∼ ΔCEF
(ii) Find AD if CE = 6 cm
(iii) If DF is parallel to BC find area of ΔADF: area of ΔABC.
In ΔABC, point D divides AB in the ratio 5:7, Find: `"AD"/"AB"`
In ΔABC, BP and CQ are altitudes from B and C on AC and AB respectively. BP and CQ intersect at O. Prove that
(i) PC x OQ = QB x OP
(ii) `"OC"^2/"OB"^2 = ("PC" xx "PO")/("QB" xx "QO")`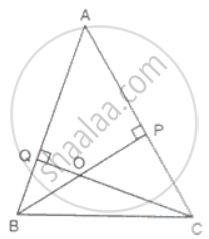
D and E are points on the sides AB and AC of ΔABC such that DE | | BC and divides ΔABC into two parts, equal in area. Find `"BD"/"AB"`.
In ΔABC, AB = 8cm, AC = 10cm and ∠B = 90°. P and Q are the points on the sides AB and AC respectively such that PQ = 3cm ad ∠PQA = 90. Find: Area of quadrilateral PBCQ: area of ΔABC.
ΔABC is enlarged, with a scale factor 5. Find: BC, f B'C' = 16cm
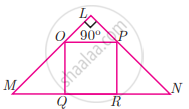
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆QMO ~ ∆RPN
Construct a triangle similar to a given triangle LMN with its sides equal to `4/5` of the corresponding sides of the triangle LMN (scale factor `4/5 < 1`)
If ∆ABC – ∆PQR in which ∠A = 53° and ∠Q = 77°, then ∠R is
If ∆ABC ~ ∆QRP, `(ar(ABC))/(ar(PQR)) = 9/4`, AB = 18 cm and BC = 15 cm, then PR is equal to ______.
