Advertisements
Advertisements
Question
In ΔABC, AB = 8cm, AC = 10cm and ∠B = 90°. P and Q are the points on the sides AB and AC respectively such that PQ = 3cm ad ∠PQA = 90. Find: Area of quadrilateral PBCQ: area of ΔABC.
Solution
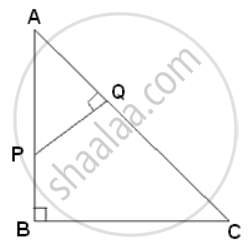
In ΔAQP and ΔABC
∠A = ∠A
∠PQA = ∠ABC ...(right angles)
Therefore, ΔAQP ∼ ΔABC
Area(trapezium EDBC) = Area(ΔABC) - Area(ΔAQP)
Area(trapezium EDBC) = 24 - 6 = 18cm2
`("Area"("trapeziumEDBC"))/("Area"(Δ"ABC")) = (18)/(24)`
⇒ `("Area"("trapeziumEDBC"))/("Area"(Δ"ABC")) = (3)/(4)`
Area(trapezium EDBC): Area(ΔABC) = 3:4.
APPEARS IN
RELATED QUESTIONS
In the following figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

Show that ΔABC, where A(–2, 0), B(2, 0), C(0, 2) and ΔPQR where P(–4, 0), Q(4, 0), R(0, 2) are similar triangles
Given: ∠GHE = ∠DFE = 90°,
DH = 8, DF = 12,
DG = 3x – 1 and DE = 4x + 2.

Find: the lengths of segments DG and DE.
In Figure 3, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and the distance between AB and DC is 14 cm. If arcs of equal radii 7 cm have been drawn, with centres A,B, C and D, then find the area of the shaded region.

In Δ ABC , MN || BC .

If BC = 14 cm and MN = 6 cm , find `("Ar" triangle "AMN")/("Ar" . ("trapezium MBCN"))`
The actual area of an island is 1872km2 . On a map, this area is 117 cm2. if the length of the coastline is 44cm on the map, find the length of its actual coastline.
In the adjoining figure. BC is parallel to DE, area of ΔABC = 25 sq cm, area of trapezium BCED = 24 sq cm, DE = 14 cm. Calculate the length of BC.
In the given figure ABC and CEF are two triangles where BA is parallel to CE and AF: AC = 5: 8.
(i) Prove that ΔADF ∼ ΔCEF
(ii) Find AD if CE = 6 cm
(iii) If DF is parallel to BC find area of ΔADF: area of ΔABC.
Find the scale factor in each of the following and state the type of size transformation:
Model volume = 200cm3, Actual volume = 8cm3
In the given figure YH || TE. Prove that ΔWHY ~ ΔWET and also find HE and TE
