Advertisements
Advertisements
Question
In ΔABC, AB = 8cm, AC = 10cm and ∠B = 90°. P and Q are the points on the sides AB and AC respectively such that PQ = 3cm ad ∠PQA = 90. Find: The area of ΔAQP.
Solution
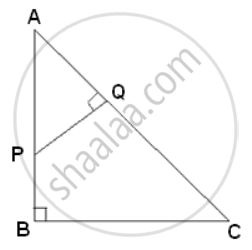
In ΔAQP and ΔABC
∠A = ∠A
∠PQA = ∠ABC ...(right angles)
Therefore, ΔAQP ∼ ΔABC
By Pythagoras theorem,
BC2 = AC2 - AB2
⇒ BC2 = 102 - 82
⇒ BC2 = 100 - 64
⇒ BC2 = 36
⇒ BC = 6cm
Area (ΔABC) `(1)/(2) xx "AB" xx "BC"`
Area (ΔABC) `(1)/(2) xx 8 xx 6`
Area (ΔABC) = 24cm2
Since ΔAQP ∼ ΔABC
`("Area"(Δ"AQP"))/("Area"(Δ"ABC")) = "PQ"^2/"BC"^2`
`("Area"(Δ"AQP"))/("Area"(Δ"ABC")) = 3^2/6^2`
⇒ Area(ΔAQP) = `(9 xx 24)/(36)`
⇒ Area(ΔAQP) = 6cm2 .
APPEARS IN
RELATED QUESTIONS
In figure, ∠A = ∠CED, prove that ∆CAB ~ ∆CED. Also, find the value of x.

ABC is a triangle. PQ is a line segment intersecting AB in P and AC in Q such that PQ || BC and divides triangle ABC into two parts equal in area. Find the value of ratio BP : AB.
In a right triangle ABC, right angled at B, D is a point on hypotenuse such that BD ⊥ AC , if DP ⊥ AB and DQ ⊥ BC then prove that
`(a) DQ^2 Dp.QC (b) DP ^2 DQ.AP 2 `

If Δ ABC , MN || BC .

If AN : AC= 5 : 8, find ar(Δ AMN) : ar(Δ ABC)
In ΔABC, BP and CQ are altitudes from B and C on AC and AB respectively. BP and CQ intersect at O. Prove that
(i) PC x OQ = QB x OP
(ii) `"OC"^2/"OB"^2 = ("PC" xx "PO")/("QB" xx "QO")`
A model of a ship is made to a scale of 1:500. Find: The length of the ship, if length of the model is 1.2.
Construct a triangle similar to a given triangle PQR with its sides equal to `7/3` of the corresponding sides of the triangle PQR (scale factor `7/3 > 1`)
In the figure, if ∠FEG ≡ ∠1 then, prove that DG2 = DE.DF
Observe the figure and complete the following activity

In fig, ∠B = 75°, ∠D = 75°
∠B ≅ [ ______ ] ...[each of 75°]
∠C ≅ ∠C ...[ ______ ]
ΔABC ~ Δ [ ______ ] ...[ ______ similarity test]
In the given figure, if ABCD is a trapezium in which AB || CD || EF, then prove that `(AE)/(ED) = (BF)/(FC)`.

