Question

D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that b² + c² = `2"p"^2 + "a"^2/2`

Answer 1

Given ∠AED = 90°

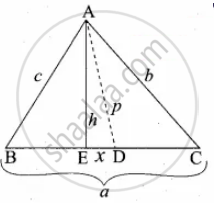
ED = x, DC = `"a"/2`    ...(D is the mid point of BC)

∴ EC = `x + "a"/2`, BE = `"a"/2 - x`

∴ In the right ∆AED

AD² = AE² + ED²

p² = h² + x²

In the right ∆AEC,

AC² = AE² + EC² 

b² = `"h"^2 + (x + "a"/2)^2`

= `"h"^2 + x^2 + "a"^2/4 + 2 xx x xx "a"/2`

b² = `"p"^2 + "a"^2/4 + "a"x`  ......(1)

b² = `"p"^2 + "a"x + 1/4 "a"^2` ....(2)

In the right triangle ABE,

AB² = AE² + BE²

c² = h² + (a2 – x)²

c² = h² + a24 + x² – ax

c² = h² + x² + 14 a² – ax

c² = p² – ax + `a^2/4` .....(3)

By adding (2) and (3)

b² + c² = `"p"^2 + "a"x + "a"^2/4 + "p"^2 - "a"x + "a"^2/4`

= `2"p"^2 + (2"a"^2)/4`

= `2"p"^2 + "a"^2/2`