Advertisements
Advertisements
प्रश्न
Observe the figure and complete the following activity
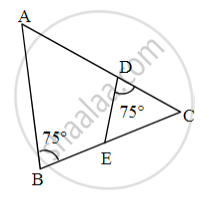
In fig, ∠B = 75°, ∠D = 75°
∠B ≅ [ ______ ] ...[each of 75°]
∠C ≅ ∠C ...[ ______ ]
ΔABC ~ Δ [ ______ ] ...[ ______ similarity test]
उत्तर
In fig, ∠B = 75°, ∠D = 75°
∠B ≅ ∠D ...[each of 75°]
∠C ≅ ∠C ...[Common angle]
ΔABC ~ ΔEDC ...[AA similarity test]]
APPEARS IN
संबंधित प्रश्न
The diagonal BD of a parallelogram ABCD intersects the segment AE at the point F, where E is any point on the side BC. Prove that DF × EF = FB × FA
In ∆ABC, DE is parallel to base BC, with D on AB and E on AC. If `\frac{AD}{DB}=\frac{2}{3}` , find `\frac{BC}{DE}.`
State, true or false:
Two similar polygons are necessarily congruent.
In the given figure, ∠ABC = 90° and BD⊥AC. If AB = 5.7cm, BD = 3.8cm and CD = 5.4cm, find BC.
In the given figure, DB⊥BC, DE⊥AB and AC⊥BC.
Prove that `(BE)/(DE)=(AC)/(BC)`
The corresponding altitudes of two similar triangles are 6cm and 9cm respectively. Find the ratio of their areas.
The dimensions of a buiIding are 50 m Iong, 40m wide and 70m high. A model of the same building is made with a scale factor of 1: 500. Find the dimensions of the model.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : BC, if B' C' = 15 cm.
In the given figure, PQ || AB; CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm. Find :
- `(CP)/(PA)`
- PQ
- If AP = x, then the value of AC in terms of x.
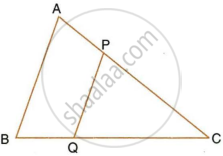
In the following figure, M is mid-point of BC of a parallelogram ABCD. DM intersects the diagonal AC at P and AB produced at E. Prove that : PE = 2 PD
Choose the correct alternative:
If ΔABC ~ ΔPQR and 4A (ΔABC) = 25 A(ΔPQR), then AB : PQ = ?
Construct a triangle ABC with side BC = 6 cm, ∠B = 45°, ∠A = 105°. Then construct another triangle whose sides are `(3)/(4)` times the corresponding sides of the ΔABC.
In the adjoining figure. BC is parallel to DE, area of ΔABC = 25 sq cm, area of trapezium BCED = 24 sq cm, DE = 14 cm. Calculate the length of BC.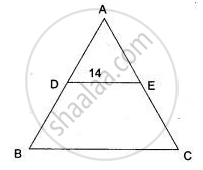
In the given figure ABC and CEF are two triangles where BA is parallel to CE and AF: AC = 5: 8.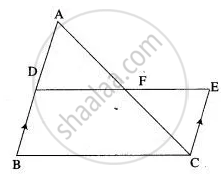
(i) Prove that ΔADF ∼ ΔCEF
(ii) Find AD if CE = 6 cm
(iii) If DF is parallel to BC find area of ΔADF: area of ΔABC.
Find the scale factor in each of the following and state the type of size transformation:
Actual area = 64m2, Model area = 100cm2
ΔABC has been reduced by a scale factor 0.6 to ΔA'B'C'/ Calculate:Length of B' C', if BC = 8cm
A vertical stick of length 6 m casts a shadow 400 cm long on the ground and at the same time a tower casts a shadow 28 m long. Using similarity, find the height of the tower
Construct a triangle similar to a given triangle LMN with its sides equal to `4/5` of the corresponding sides of the triangle LMN (scale factor `4/5 < 1`)
If in triangles ABC and EDF, `"AB"/"DE" = "BC"/"FD"` then they will be similar, when
In ∆LMN, ∠L = 60°, ∠M = 50°. If ∆LMN ~ ∆PQR then the value of ∠R is
