Advertisements
Advertisements
प्रश्न
In figure, if PQRS is a parallelogram and AB || PS, then prove that OC || SR.
उत्तर
According to the question,
PQRS is a parallelogram,
Therefore, PQ || SR and PS || QR.
Also given, AB || PS.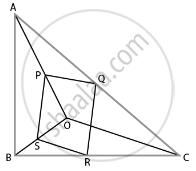
To prove:
OC || SR
From ∆OPS and OAB,
PS || AB
∠POS = ∠AOB ...[Common angle]
∠OSP = ∠OBA ...[Corresponding angles]
∴ ∆OPS ∼ ∆OAB ...[By AAA similarity criteria]
Then,
Using basic proportionality theorem,
We get,
`("PS")/("AB") = ("OS")/("OB")` ...(i)
From ∆CQR and ∆CAB,
QR || PS || AB
∠QCR = ∠ACB ...[Common angle]
∠CRQ = ∠CBA ...[Corresponding angles]
∴ ∆CQR ∼ ∆CAB
Then, by basic proportionality theorem
`("QR")/("AB") = ("CR")/("CB")`
⇒ `("PS")/("AB") = ("CR")/("CB")` ...(ii) [PS ≅ QR Since, PQRS is a parallelogram]
From equations (i) and (ii),
`("OS")/("OB") = ("CR")/("CB")`
or
`("OB")/("OS") = ("CB")/("CR")`
Subtracting 1 from L.H.S and R.H.S, we get,
`("OB")/("OS") - 1 = ("CB")/("CR") - 1`
⇒ `("OB" - "OS")/("OS") = ("CB" - "CR")/("CR")`
⇒ `("BS")/("OS") = ("BR")/("CR")`
SR || OC ...[By converse of basic proportionality theorem]
Hence proved.
APPEARS IN
संबंधित प्रश्न
Prove that the angle bisector of a triangle divides the side opposite to the angle in the ratio of the remaining sides.
In figure, if ∠A = ∠C, then prove that ∆AOB ~ ∆COD

Using Converse of basic proportionality theorem, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).
In the given figure ΔABC and ΔAMP are right angled at B and M respectively. Given AC = 10 cm, AP = 15 cm and PM = 12 cm.

1) Prove ΔABC ~ ΔAMP
2) Find AB and BC.
Given: FB = FD, AE ⊥ FD and FC ⊥ AD.
Prove that: `(FB)/(AD) = (BC)/(ED)`.

Area of two similar triangles are 98 sq. cm and 128 sq. cm. Find the ratio between the lengths of their corresponding sides.
The corresponding sides of two similar triangles ABC and DEF are BC = 9.1cm and EF = 6.5cm. If the perimeter of ΔDEF is 25cm, find the perimeter of ΔABC.
In a circle, two chords AB and CD intersect at a point P inside the circle. Prove that
(a) ΔPAC ∼PDB (b) PA. PB= PC.PD

Two chords AB and CD of a circle intersect at a point P outside the circle.
Prove that: (i) Δ PAC ~ Δ PDB (ii) PA. PB = PC.PD

As shown in figure, two poles of height 8 m and 4 m are perpendicular to the ground. If the length of shadow of smaller pole due to sunlight is 6 m then how long will be the shadow of the bigger pole at the same time?


O is any point in the interior of ΔABC. Bisectors of ∠AOB, ∠BOC and ∠AOC intersect side AB, side BC, side AC in
F, D and E respectively.
Prove that
BF × AE × CD = AF × CE × BD
In Δ ABC, DE || BC; DC and EB intersects at F. if `"DE"/"BC" = 2/7` , find `("Ar" (triangle "FDE"))/("Ar" (triangle "FBC"))`
Figure shows Δ KLM , P an T on KL and KM respectively such that∠ KLM =∠ KTP.
If `"KL"/"KT" = 9/5` , find `("Ar" triangle "KLM")/("Ar" triangle "KTP")`.

AD and BC are two straight lines intersecting at 0. CD and BA are perpendirulars from Band Con AD. If AB=6cm, CD =9cm, AD =20cm and BC=25cm, find the lengths of AO, BO, CO and DO.
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The area in km2 that can be represented by 1 cm2
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in m, of the aeroplane, if length of its model is 16 cm.
In the following figure, point D divides AB in the ratio 3 : 5. Find :
BC = 4.8 cm, find the length of DE.

In ΔABC, D and E are the points on sides AB and AC respectively. Find whether DE || BC, if AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and AE = 1.6 cm.
Find the scale factor in each of the following and state the type of size transformation:
Image length = 6cm, Actual length = 4cm.
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The length of the truck
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The base area of the truck, if the base area of the model is 30m2
A vertical stick of length 6 m casts a shadow 400 cm long on the ground and at the same time a tower casts a shadow 28 m long. Using similarity, find the height of the tower
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that c2 = `"p"^2 - "a"x + "a"^2/4`
In the given figure YH || TE. Prove that ΔWHY ~ ΔWET and also find HE and TE
ΔABC ~ ΔPQR, A(ΔABC) = 80 sq.cm, A(ΔPQR) = 125 sq.cm, then complete `("A"(Δ"ABC"))/("A"(Δ"PQR")) = 80/125 = (["______"])/(["______"])`, hence `"AB"/"PQ" = (["______"])/(["______"])`
In fig., seg AC and seg BD intersect each other at point P.

`"AP"/"PC" = "BP"/"PD"` then prove that ΔABP ~ ΔCDP
ΔABC and ΔBDE are two equilateral triangles such that D is the mid point of BC. Ratio of the areas of triangle ΔABC and ΔBDE is ______.
