Advertisements
Advertisements
प्रश्न
A vertical stick of length 6 m casts a shadow 400 cm long on the ground and at the same time a tower casts a shadow 28 m long. Using similarity, find the height of the tower
उत्तर
In ∆ABC and ∆PQR,
∠ABC = ∠PQR = 90° ...(Vertical Stick)
∠ACB = ∠PRQ ...(Same time casts shadow)
∆BCA ~ ∆QRP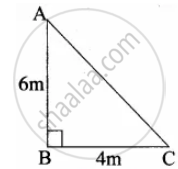
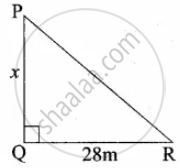
`"AB"/"PQ" = "NC"/"QR"`
`6/x = 4/28`
4x = 6 × 28
⇒ x = `(6 xx 28)/4` = 42
Length of the lamp post = 42 m
APPEARS IN
संबंधित प्रश्न
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :

- ΔADE ∼ ΔACB.
- If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
- Find, area of ΔADE : area of quadrilateral BCED.
ΔABC ∼ ΔDEF and A(ΔABC) : A Δ(DEF) = 1 : 2 If AB = 4 find DE.
In Δ ABC, DE || BC; DC and EB intersects at F. if `"DE"/"BC" = 2/7` , find `("Ar" (triangle "FDE"))/("Ar" (triangle "FBC"))`
Δ ABC is similar to Δ PQR. If AB = 6cm, BC = 9cm, PQ = 9cm and PR = 10.5cm, find the lengths of AC and QR.
Find the area of the triangle ABC with the coordinates of A as (1, −4) and the coordinates of the mid-points of sides AB and AC respectively are (2, −1) and (0, −1).
In the adjoining figure. BC is parallel to DE, area of ΔABC = 25 sq cm, area of trapezium BCED = 24 sq cm, DE = 14 cm. Calculate the length of BC.
Find the scale factor in each of the following and state the type of size transformation:
Model area = 75cm2, Actual area = 3cm2
A girl looks the reflection of the top of the lamp post on the mirror which is 6.6 m away from the foot of the lamppost. The girl whose height is 1.25 m is standing 2.5 m away from the mirror. Assuming the mirror is placed on the ground facing the sky and the girl, mirror and the lamppost are in the same line, find the height of the lamp post.
If BD ⊥ AC and CE ⊥ AB, prove that `"CA"/"AB" = "CE"/"DB"`

D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that b2 = `"p"^2 + "a"x + "a"^2/4`
