Advertisements
Advertisements
प्रश्न
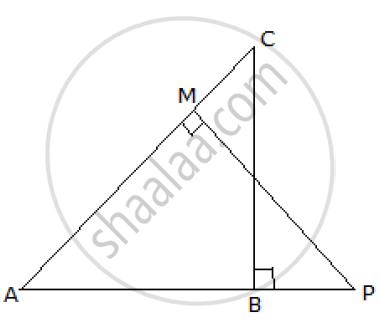
In the given figure ΔABC and ΔAMP are right angled at B and M respectively. Given AC = 10 cm, AP = 15 cm and PM = 12 cm.

1) Prove ΔABC ~ ΔAMP
2) Find AB and BC.
उत्तर
In ABC and AMP
∠ABC = ∠AMP (each 90°)
∠BAC = ∠PAM (common)
∴ΔABC ~ ΔAMP (By AA similarity)
Since the triangles are similar, we have
`(AB)/(AM) = (BC)/(MP) = (AC)/(AP)`
`=> (AB)/(AM) = (BC)/(MP) = (AC)/(AP)`
`=> (AB)/(AM) = (BC)/12 = 10/15`
Taking `(BC)/12 = 10/15 => BC = (12 xx 10)/15` = 8 cm
Now, using Pythagoras theorem in ΔABC
`(AB)^2 + (BC)^2 = (AC)^2`
`=> (AB)^2 = 10^2 - 8^2 = 36`
=> AB = 6 cm
Hence AB = 6 cm and BC = 8 cm
APPEARS IN
संबंधित प्रश्न
In figure, find ∠L

The areas of two similar triangles are `81cm^2` and `49cm^2` respectively. If the altitude of the first triangle is 6.3cm, find the corresponding altitude of the other.
State the SSS-similarity criterion for similarity of triangles
In the figure, parts of the two triangles bearing identical marks are
congruent. State the test by which the triangles are congruent.

In figure , DEF is a right -angled triangle with ∠ E = 90 °.FE is produced to G and GH is drawn perpendicular to DE = 8 cm , DH = 8 cm ,DH = 6 cm and HF = 4 cm , find `("Ar" triangle "DEF")/("Ar" triangle "GHF")`

A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : A' B', if AB = 4 cm.
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in cm, of the model; if the length of the aeroplane is 40 m.
In a right-angled triangle ABC, ∠B = 90°, P and Q are the points on the sides AB and AC such as PQBC, AB = 8 cm, AQ = 6 cm and PA:AB = 1:3. Find the lengths of AC and BC.
Two triangles QPR and QSR, right angled at P and S respectively are drawn on the same base QR and on the same side of QR. If PR and SQ intersect at T, prove that PT × TR = ST × TQ
Two similar triangles will always have ________ angles
