Question

In figure, if PQRS is a parallelogram and AB || PS, then prove that OC || SR.

Answer 1

According to the question,

PQRS is a parallelogram,

Therefore, PQ || SR and PS || QR.

Also given, AB || PS.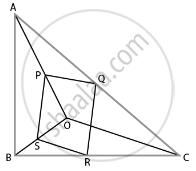

To prove:

OC || SR

From ∆OPS and OAB,

PS || AB

∠POS = ∠AOB ...[Common angle]

∠OSP = ∠OBA   ...[Corresponding angles]

∴ ∆OPS ∼ ∆OAB   ...[By AAA similarity criteria]

Then,

Using basic proportionality theorem,

We get,

`("PS")/("AB") = ("OS")/("OB")`   ...(i)

From ∆CQR and ∆CAB,

QR || PS || AB

∠QCR = ∠ACB   ...[Common angle]

∠CRQ = ∠CBA   ...[Corresponding angles]

∴ ∆CQR ∼ ∆CAB

Then, by basic proportionality theorem

`("QR")/("AB") = ("CR")/("CB")`

⇒ `("PS")/("AB") = ("CR")/("CB")`  ...(ii) [PS ≅ QR Since, PQRS is a parallelogram]

From equations (i) and (ii),

`("OS")/("OB") = ("CR")/("CB")`

or

`("OB")/("OS") = ("CB")/("CR")`

Subtracting 1 from L.H.S and R.H.S, we get,

`("OB")/("OS") - 1 = ("CB")/("CR") - 1`

⇒ `("OB" - "OS")/("OS") = ("CB" - "CR")/("CR")`

⇒ `("BS")/("OS") = ("BR")/("CR")`

SR || OC  ...[By converse of basic proportionality theorem]

Hence proved.