Advertisements
Advertisements
प्रश्न
Δ ABC ∼ Δ PQR such that AB= 1.5 cm and PQ=2. 1 cm. Find the ratio of areas of Δ ABC and ΔPQR.
उत्तर
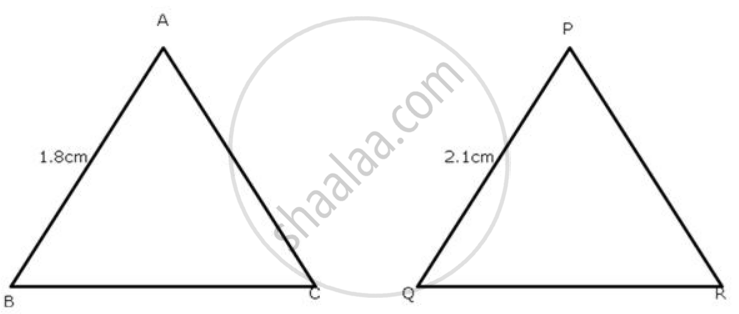
To find : `("Ar" triangle "ABC")/("Ar" triangle "PQR") = "AB"^2/"PQ"^2`
[The ration of areas of two similar triangle is equal to the ratio of square of their corresponding sides.]
`= (1.8/2.1)^2`
`= (6/7)^2`
`= 36/49`
Required ratio = 36 : 49.
APPEARS IN
संबंधित प्रश्न
Prove that the angle bisector of a triangle divides the side opposite to the angle in the ratio of the remaining sides.
In the given figure ABC is a triangle with ∠EDB = ∠ACB. Prove that Δ ABC ~ Δ EBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm. And area of Δ BED = 9 cm2. Calculate the
(1) length of AB
(2) area of Δ ABC

Area of two similar triangles are 98 sq. cm and 128 sq. cm. Find the ratio between the lengths of their corresponding sides.
ΔABC is right angled at A and AD⊥BC. If BC = 13cm and AC = 5cm, find the ratio of the areas of ΔABC and ΔADC.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : OA, if OA' = 6 cm.
In the following figure, point D divides AB in the ratio 3 : 5. Find :
DE = 2.4 cm, find the length of BC.

In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD : BD = 4 : 5 and EC = 2.5cm, find AE.
The areas of two similar triangles are 16cm2 and 9cm2 respectively. If the altitude of the smaller triangle is 1.8cm, find the length of the altitude corresponding to the larger triangle.
Find the scale factor in each of the following and state the type of size transformation:
Image length = 6cm, Actual length = 4cm.
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that c2 = `"p"^2 - "a"x + "a"^2/4`
