Advertisements
Advertisements
प्रश्न
Δ ABC ∼ Δ PQR such that AB= 1.5 cm and PQ=2. 1 cm. Find the ratio of areas of Δ ABC and ΔPQR.
उत्तर
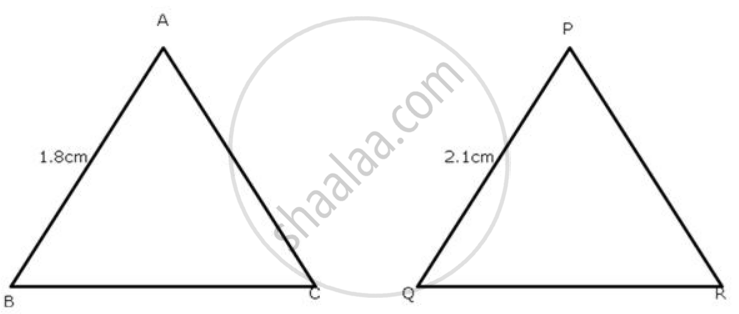
To find : `("Ar" triangle "ABC")/("Ar" triangle "PQR") = "AB"^2/"PQ"^2`
[The ration of areas of two similar triangle is equal to the ratio of square of their corresponding sides.]
`= (1.8/2.1)^2`
`= (6/7)^2`
`= 36/49`
Required ratio = 36 : 49.
APPEARS IN
संबंधित प्रश्न
In figure, find ∠L

In the given figure, ∠ABC = 90° and BD⊥AC. If AB = 5.7cm, BD = 3.8cm and CD = 5.4cm, find BC.
Δ ABC ∼ Δ PQR. AD and PS are altitudes from A and P on sides BC and QR respectively. If AD : PS = 4 : 9 , find the ratio of the areas of Δ ABC and Δ PQR.
Figure shows Δ KLM , P an T on KL and KM respectively such that∠ KLM =∠ KTP.
If `"KL"/"KT" = 9/5` , find `("Ar" triangle "KLM")/("Ar" triangle "KTP")`.

The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The number of kilometres on the ground represented by lcm or the map
If ΔABC ~ ΔDEF, then writes the corresponding congruent angles and also write the ratio of corresponding sides.
In the given figure, AB and DE are perpendicular to BC.

- Prove that ΔABC ∼ ΔDEC
- If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
- Find the ratio of the area of a ΔABC : area of ΔDEC.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 4, AE = 8, DB = x - 4 and EC = 3x - 19, find x.
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆LOP ~ ∆QMO

If ΔABC ∼ ΔDEF and ∠A = 48°, then ∠D = ______.
