Advertisements
Advertisements
Question
AD and BC are two straight lines intersecting at 0. CD and BA are perpendirulars from Band Con AD. If AB=6cm, CD =9cm, AD =20cm and BC=25cm, find the lengths of AO, BO, CO and DO.
Solution
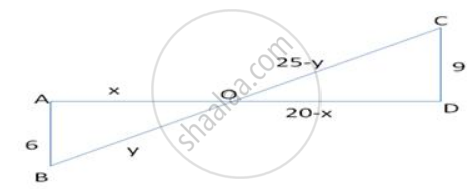
To find : AO , BO , CO , DO
In Δ AOB and Δ COD
∠OAB = ∠ ODC (90° each)
∠ AOB = ∠ DOC (vertically opposite angles)
∴ Δ AOB ∼ Δ DOC (AA corollary)
`therefore "AO"/"DO" = "OB"/"OC" = "AB"/"DC"`
`"x"/(20 - "x") = "y"/(25 - "y") = 6/9`
`"x"/(20 - "x") = 2/3 , "y"/(25 - "y") = 2/3`
3x = 40 - 2x , 3y = 50 - 2y
5x = 40 , 5y = 50
x = 8 , y = 10
AO = 8 xm , OB = 10 cm
OD = 20 - 8 = 12 cm , OC = 25 - 10 = 15 cm
APPEARS IN
RELATED QUESTIONS
Using Converse of basic proportionality theorem, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).
State, true or false:
All equiangular triangles are similar.
In triangle ABC, DE is parallel to BC; where D and E are the points on AB and AC respectively.
Prove: ∆ADE ~ ∆ABC.
Also, find the length of DE, if AD = 12 cm, BD = 24 cm BC = 8 cm.
The corresponding altitudes of two similar triangles are 6cm and 9cm respectively. Find the ratio of their areas.
In Δ ABC , DE is parallel to BC and `"AD"/"DB" = 2/7` IF AC = 5 .6 , find AE.
Construct a ΔABC in which CA = 6 cm, AB = 5 cm and ∠BAC = 45°. Then construct a triangle whose sides are `3/5` of the corresponding sides of ΔABC.
Let ∆ ABC ∽ ∆ DEF and their areas be respectively, 64 cm2 and 121 cm2. If EF = 15⋅4 cm, find BC.
Check whether the triangles are similar and find the value of x
In the figure, which of the following statements is true?
Areas of two similar triangles are 225 cm2 and 81 cm2. If side of smaller triangle is 12 cm, find corresponding side of major triangle.
