English Medium
Academic Year: 2022-2023
Date & Time: 21st March 2023, 10:30 am
Duration: 3h
Advertisements
General Instructions:
- This question paper contains 38 questions. All questions are compulsory.
- This Question Paper is divided into FIVE Sections - Section A, B, C, D, and E.
- In Section - A question number 1 to 18 are Multiple Choice Questions (MCQs) and question number 19 & 20 are Assertion Reason based questions of 1 mark each.
- In Section - B questions number 21 to 25 are Very Short Answer (VSA) type questions of 2 marks each.
- In Section - C questions number 26 to 31 are Short Answer-II (SA) type questions carrying 3 marks each.
- In Section - D questions number 32 to 35 are Long Answer (LA) type questions carrying 5 marks each.
- In Section - E questions number 36 to 38 are Case Study/Passage based integrated units and assessment questions carrying 4
marks each. Internal choice is provided in 2 marks questions in each case study. - There is no overall choice. However, an internal choice has been provided in 2 questions in Section B, 2 questions in Section C, 2 questions in Section D, and 3 questions in Section E.
- Draw neat figures wherever required. Take π = `22/7` wherever required if not stated.
- Use of calculator is NOT allowed.
The time, in seconds, taken by 150 athletes to run a 100 m hurdle race are tabulated below:
| Time (sec.) | 13 – 14 | 14 – 15 | 15 – 16 | 16 – 17 | 17 – 18 | 18 – 19 |
| Number of Athletes | 2 | 4 | 5 | 71 | 48 | 20 |
The number of athletes who completed the race in less than 17 seconds is:
11
71
82
68
Chapter: [0.071] Statistics [0.071] Statistics
The distance of the point (5, 0) from the origin is ______.
0
5
`sqrt(5)`
52
Chapter: [0.031] Lines (In Two-dimensions)
In ΔBC, right angled at C, if tan A = `8/7`, then the value of cot B is ______.
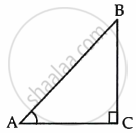
`7/8`
`8/7`
`7/sqrt(113)`
`8/sqrt(113)`
Chapter: [0.051] Introduction to Trigonometry
Area of a quadrant of a circle of radius 7 cm is ______.
154 cm2
77 cm2
`77/2`cm2
`77/4`cm2
Chapter: [0.061] Areas Related to Circles
If HCF (72, 120) = 24, then LCM (72, 120) is ______.
72
120
360
9640
Chapter: [0.011000000000000001] Real Numbers
One card is drawn at random from a well-shuffled deck of 52 playing cards. What is the probability of getting a black king?
`1/26`
`1/13`
`1/52`
`1/2`
Chapter: [0.07200000000000001] Probability
The graph of y = f(x) is shown in the figure for some polynomial f(x).
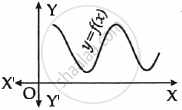
The number of zeroes of f(x) is ______.
0
2
3
4
Chapter: [0.021] Polynomials
The value of k, if (6, k) lies on the line represented by x – 3y + 6 = 0, is ______.
– 4
12
– 12
4
Chapter:
The prime factorisation of the number 2304 is ______.
28 × 32
27 × 33
28 × 31
27 × 32
Chapter: [0.011000000000000001] Real Numbers
If n is a natural number, then 8n cannot end with digit
0
2
4
6
Chapter: [0.011000000000000001] Real Numbers
The median of first seven prime numbers is ______.
5
7
11
13
Chapter: [0.071] Statistics
If (2, 4) is the mid-point of the line segment joining (6, 3) and (a, 5), then the value of a is ______.
2
4
– 4
– 2
Chapter: [0.031] Lines (In Two-dimensions)
The value of ‘k’ for which the system of equations kx + 2y = 5 and 3x + 4y = 1 have no solution, is ______.
k = `3/2`
k ≠ `3/2`
k ≠ `2/3`
k = 15
Chapter:
In the given figure, PQ and PR are tangents drawn from P to the circle with centre O such that ∠QPR = 65°. The measure of ∠QOR is ______.
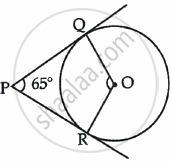
65°
125°
115°
90°
Chapter: [0.042] Circles
The zeroes of the quadratic polynomial 16x2 – 9 are ______.
`3/4, 3/4`
`-3/4, 3/4`
`9/16, 9/16`
`-3/4, -3/4`
Chapter: [0.021] Polynomials
If –5, x, 3 are three consecutive terms of an A.P., then the value of x is ______.
– 2
2
1
– 1
Chapter: [0.024] Arithmetic Progressions
An unbiased die is thrown. The probability of getting an odd prime number is ______.
`1/6`
`1/2`
`2/3`
`1/3`
Chapter: [0.07200000000000001] Probability
Advertisements
If the mean of 6, 7, x, 8, y, 14 is 9, then ______.
x + y = 21
x + y = 19
x − y = 19
x − y = 21
Chapter: [0.071] Statistics
Assertion (A): The probability that a leap year has 53 Sundays is `2/7`.
Reason (R): The probability that a non-leap year has 53 Sundays is `1/2`.
Both Assertion (A) and Reason (R) are true; and Reason (R) is the correct explanation of Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of Assertion (A).
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Chapter: [0.07200000000000001] Probability
Assertion (A): For 0 < 0 ≤ 90°, cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other.
Reason (R): cot2 θ – cosec2 θ = 1.
Both Assertion (A) and Reason (R) are true; and Reason (R) is the correct explanation of Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of Assertion (A).
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Chapter: [0.051] Introduction to Trigonometry
Evaluate: 5 cosec2 45° – 3 sin2 90° + 5 cos 0°.
Chapter: [0.051] Introduction to Trigonometry
Find a quadratic polynomial whose zeroes are 6 and – 3.
Chapter: [0.021] Polynomials
Find the zeroes of the polynomial x2 + 4x – 12.
Chapter: [0.021] Polynomials
Find the value of k for which the roots of the quadratic equation 5x2 – 10x + k = 0 are real and equal.
Chapter: [0.023] Quadratic Equations
If one root of the quadratic equation 3x2 – 8x – (2k + 1) = 0 is seven times the other, then find the value of k.
Chapter: [0.023] Quadratic Equations
A box contains 20 discs which are numbered from 1 to 20. If one disc is drawn at random from the box, then find the probability that the number the drawn disc is a 2-digit number.
Chapter: [0.07200000000000001] Probability
A box contains 20 discs which are numbered from 1 to 20. If one disc is drawn at random from the box, then find the probability that the number the drawn disc is a number less than 10.
Chapter: [0.07200000000000001] Probability
From a point P, the length of the tangent to a circle is 24 cm and the distance of P from the centre of the circle is 25 cm. Find the radius of the circle.
Chapter: [0.042] Circles
The sum of the reciprocals of Varun's age (in years) 3 years ago and 5 years from now is `1/3`. Find his present age.
Chapter: [0.023] Quadratic Equations
A survey conducted on 20 households in a locality by a group of students resulted in the following frequency table for the number of family members in a household:
| Family size | 1 – 3 | 3 – 5 | 5 – 7 | 7 – 9 | 9 – 11 |
| Numbers of Families | 7 | 8 | 2 | 2 | 1 |
Find the median of this data.
Chapter: [0.071] Statistics
Advertisements
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE ∼ ΔCFB.
Chapter: [0.040999999999999995] Triangles
In the given figure, CM and RN are respectively the medians of ΔABC and ΔPQR. If ΔABC ∼ ΔPQR, then prove that ΔAMC ∼ ΔPNR.
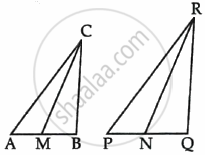
Chapter: [0.040999999999999995] Triangles
Find the co-ordinates of the points of trisection of the line segment joining the points (5, 3) and (4, 5).
Chapter: [0.031] Lines (In Two-dimensions)
Prove that `3 - 2sqrt(5)` is an irrational number, given that `sqrt(5)` is an irrational number.
Chapter: [0.011000000000000001] Real Numbers
Prove that `(cot A - cos A)/(cot A + cos A) = (cos^2 A)/(1 + sin A)^2`
Chapter: [0.051] Introduction to Trigonometry [0.052000000000000005] Trigonometric Identities
Prove that (sec θ + tan θ) (1 – sin θ) = cos θ
Chapter: [0.051] Introduction to Trigonometry [0.052000000000000005] Trigonometric Identities
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks, find the width of the river. (Use `sqrt(3)` = 1.73)
Chapter: [0.053] Some Applications of Trigonometry
From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower. (Use `sqrt3` = 1.73)
Chapter: [0.053] Some Applications of Trigonometry
The first term of an A.P. is 22, the last term is –6 and the sum of all the terms is 64. Find the number of terms of the A.P. Also, find the common difference.
Chapter: [0.024] Arithmetic Progressions
An ice-cream filled cone having radius 5 cm and height 10 cm is as shown in the figure. Find the volume of the ice-cream in 7 such cones.

Chapter: [0.062] Surface Areas and Volumes
Prove that, if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.
Chapter: [0.040999999999999995] Triangles [0.040999999999999995] Triangles [0.040999999999999995] Triangles
In the following figure, `("QR")/("QS") = ("QT")/("PR")` and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR.

Chapter: [0.040999999999999995] Triangles
Read the following passage:
|
For the inauguration of 'Earth day' week in a school, badges were given to volunteers. Organisers purchased these badges from an NGO, who made these badges in the form of a circle inscribed in a square of side 8 cm.
|
Based on the above information, answer the following questions:
- What is the area of square ABCD?
- What is the length of diagonal AC of square ABCD?
- Find the area of sector OPRQO.
OR
Find the area of remaining part of square ABCD when area of circle is excluded.
Chapter: [0.061] Areas Related to Circles
Read the following passage:
 Lokesh, a production manager in Mumbai, hires a taxi everyday to go to his office. The taxi charges in Mumbai consists of a fixed charges together with the charges for the distance covered. His office is at a distance of 10 km from his home. For a distance of 10 km to his office, Lokesh paid ₹ 105. While coming back home, he took another roµte. He covered a distance of 15 km and the charges paid by him were ₹ 155. |
Based on the above information, answer the following questions:
- What are the fixed charges?
- What are the charges per km?
- If fixed charges are ₹ 20 and charges per km are ₹ 10, then how much Lokesh have to pay for travelling a distance of 10 km?
OR
Find the total amount paid by Lokesh for travelling 10 km from home to office and 25 km from office to home. [Fixed charges and charges per km are as in (i) and (ii).
Chapter: [0.022000000000000002] Pair of Linear Equations in Two Variables
Read the following passage:
People of a circular village Dharamkot want to construct a road nearest to it. The road cannot pass through the village. But the people want the road at a shortest distance from the centre of the village. Suppose the road starts from A which is outside the circular village (as shown in the figure) and touch the boundary of the circular village at B such that AB = 20 m. Also the distance of the point A from the centre O of the village is 25 m. |
Based on the above information, answer the following questions:
- If B is the mid-point of AC, then find the distance AC.
- Find the shortest distance of the road from the centre of the village.
- Find the circumference of the village.
OR
Find the area of the village.
Chapter: [0.061] Areas Related to Circles
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
CBSE previous year question papers Class 10 Mathematics with solutions 2022 - 2023
Previous year Question paper for CBSE Class 10 Maths-2023 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of CBSE Class 10.
How CBSE Class 10 Question Paper solutions Help Students ?
• Question paper solutions for Mathematics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.




