Advertisements
Advertisements
Question
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks, find the width of the river. (Use `sqrt(3)` = 1.73)
Solution
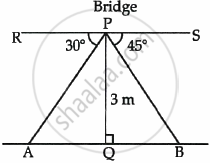
Let the width of the river be x m
i.e., AB = x m
P is the point on the bridge
∴ PQ = 3 m
and ∠RPA = 30° and ∠SPB = 45°
In ΔAPQ, ∠Q = 90° ∠A = 30°
tan A = `(PQ)/(AQ)`
tan 30° = `3/(AQ)`
`1/sqrt(3) = 3/(AQ)`
∴ AQ = `3sqrt(3)` m ...(1)
In ΔPQB, ∠Q = 90° ∠B = 45°
tan B = `(PQ)/(BQ)`
tan 45° = `3/(BQ)`
1 = `3/(BQ)`
BQ = 3 ...(2)
AB = AQ + BQ
= `3sqrt(3) + 3`
= `3(sqrt(3) + 1)` m
Width of River = `3(sqrt(3) + 1)`
= 3 × 2.73
= 8.19 m.
APPEARS IN
RELATED QUESTIONS
On a straight line passing through the foot of a tower, two points C and D are at distances of 4 m and 16 m from the foot respectively. If the angles of elevation from C and D of the top of the tower are complementary, then find the height of the tower.
PQ is a post of given height a, and AB is a tower at some distance. If α and β are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
The angles of elevation of the top of a rock from the top and foot of a 100 m high tower are respectively 30° and 45°. Find the height of the rock.
A solid right-circular cone of height 60 cm and radius 30 cm is dropped in a right-circular cylinder full of water of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder, in cubic metres ?
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of depression from the top of the tower to the foot of the hill is 30°. If the tower is 50 m high, find the height of the hill ?
A person is standing at a distance of 80 m from a church looking at its top. The angle of elevation is of 45°. Find the height of the church.
The lower window of a house is at a height of 2 m above the ground and its upper window is 4 m vertically above the lower window. At certain instant the angles of elevation of a balloon from these windows are observed to be 60° and 30° respectively. Find the height of the balloon above the ground.
The angles of depression of the top and the bottom of a 10 m tall building from the top of a multi-storeyed building are 30° and 45°, respectively. Find the height of the multi-storeyed building.
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will also be doubled.
A window of a house is h metres above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be α and β, respectively. Prove that the height of the other house is h(1+ tan α tan β) metres.
