Advertisements
Advertisements
प्रश्न
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks, find the width of the river. (Use `sqrt(3)` = 1.73)
उत्तर
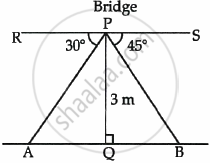
Let the width of the river be x m
i.e., AB = x m
P is the point on the bridge
∴ PQ = 3 m
and ∠RPA = 30° and ∠SPB = 45°
In ΔAPQ, ∠Q = 90° ∠A = 30°
tan A = `(PQ)/(AQ)`
tan 30° = `3/(AQ)`
`1/sqrt(3) = 3/(AQ)`
∴ AQ = `3sqrt(3)` m ...(1)
In ΔPQB, ∠Q = 90° ∠B = 45°
tan B = `(PQ)/(BQ)`
tan 45° = `3/(BQ)`
1 = `3/(BQ)`
BQ = 3 ...(2)
AB = AQ + BQ
= `3sqrt(3) + 3`
= `3(sqrt(3) + 1)` m
Width of River = `3(sqrt(3) + 1)`
= 3 × 2.73
= 8.19 m.
APPEARS IN
संबंधित प्रश्न
On a horizontal plane, there is a vertical tower with a flagpole on the top of the tower. At a point 9 meters away from the foot of the tower the angle of elevation of the top and bottom of the flagpole are 60° and 30° respectively. Find the height of the tower and the flagpole mounted on it.
The angles of depression of two ships from the top of a lighthouse and on the same side of it are found to be 45° and 30° respectively. If the ships are 200 m apart, find the height of the lighthouse.
The angle of elevation of the top of a tower from ta point on the same level as the foot of the tower is 30° . On advancing 150 m towards foot of the tower, the angle of elevation becomes 60° Show that the height of the tower is 129.9 metres.
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angels of elevation of the top of the poles are 60° and 30° respectively.
Find the height of the poles and the distances of the point from the poles.
A kite is flying at a height of 45 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is
60°. Find the length of the string assuming that there is no slack in the string.
If the angle of elevation of a cloud from a point 200 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°, then the height of the cloud above the lake is
From the top of a rock `50sqrt(3)` m high, the angle of depression of a car on the ground is observed to be 30°. Find the distance of the car from the rock
As observed from the top of a 150 m high lighthouse from the sea level, the angles of depression of the two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
A kite is flying at a height of 30 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
The angles of elevation of the top of a tower from two points distant s and t from its foot are complementary. Then the height of the tower is ____________.
