Advertisements
Advertisements
प्रश्न
The angles of depression of two ships from the top of a lighthouse and on the same side of it are found to be 45° and 30° respectively. If the ships are 200 m apart, find the height of the lighthouse.
उत्तर

Let CD be the light house and A and B be the positions of the two ships.
AB = 200 m (Given)
Suppose CD = h m and BC = x m
Now,
∠DAC = ∠ADE = 30º (Alternate angles)
∠DBC =∠EDB = 45º (Alternate angles)
In right ∆BCD,
`tan 45^@ = (CD)/(BC)`
`=> 1 = h/x`
=> x = h .....(1)
In right ∆ACD,
`tan 30^@ = (CD)/(AC)`
`=> 1/sqrt3 = h/(x + 200)`
` => sqrt3h = x + 200` ......(2)
From (1) and (2), we get
`sqrt3h = 200 + h`
`=> sqrt3h - h = 200`
`=> (sqrt3 - 1)h = 200``
`=> h = 200/(sqrt3 - 1)`
`=> h = (200(sqrt3 + 1))/(((sqrt3 -1)(sqrt3 + 1))`
`=> h = (200(sqrt3 + 1))/2 = 100(sqrt3 + 1)`m
Hence, the height of the light house is `100(sqrt3 + 1)` m
संबंधित प्रश्न
If the angle of elevation of cloud from a point 200 m above a lake is 30º and the angle of depression of its reflection in the lake is 60º, then find the height of the cloud above the lake
The angle of elevation of the top of a tower as observed form a point in a horizontal plane through the foot of the tower is 32°. When the observer moves towards the tower a distance of 100 m, he finds the angle of elevation of the top to be 63°. Find the height of the tower and the distance of the first position from the tower. [Take tan 32° = 0.6248 and tan 63° = 1.9626]
An observed from the top of a 150 m tall lighthouse, the angles of depression of two ships approaching it are 30° and 45°. If one ship is directly behind the other, find the distance between the two ships.
The vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height 6m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is
30 and that of the top of the flagstaff 60 . Find the height of the tower
[Use `sqrt(3)` 1.732 ]
The angle of elevation on the top of a building from the foot of a tower is 30° . The angle of elevation of the top of the tower when seen from the top of the second water is 60° .If the tower is 60m high, find the height of the building.
The angle of elevation of an aeroplane from a point on the ground is 45° after flying for 15seconds, the elevation changes to 30° . If the aeroplane is flying at a height of 2500 meters, find the speed of the areoplane.
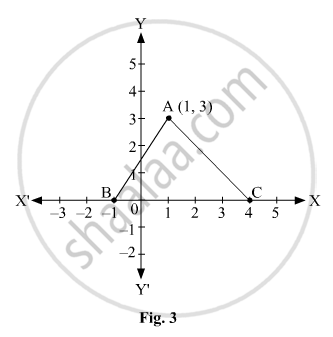
In Fig. 3, the area of triangle ABC (in sq. units) is:
From a point on the ground, 20 m away from the foot of a vertical tower, the angle elevation of the top of the tower is 60°, What is the height of the tower?
If the angle of elevation of a tower from a distance of 100 metres from its foot is 60°, then the height of the tower is
Two vertical poles are 150 m apart and the height of one is three times that of the other. If from the middle point of the line joining their feet, an observer finds the angles of elevation of their tops to be complementary, then the height of the shorter pole (in meters) is ______.
