Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a tower as observed form a point in a horizontal plane through the foot of the tower is 32°. When the observer moves towards the tower a distance of 100 m, he finds the angle of elevation of the top to be 63°. Find the height of the tower and the distance of the first position from the tower. [Take tan 32° = 0.6248 and tan 63° = 1.9626]
उत्तर
Let h be the height of the tower and the angle of elevation as observed from the foot of the tower is 32° and observed move towards the tower with distance 100 m then the angle of elevation becomes 63°.
Let BC = x and CD = 100
Now we have to find the height of the tower
So we use trigonometrical ratios.
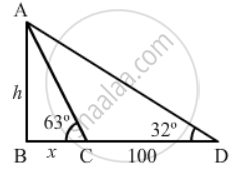
In a triangle ABC,
`=> tan C = (AB)/(BC)`
`=> tan 63^@ = (AB)/(BC)`
`=> 1.9626 = h/x`
`=> x = h/1.9626`
Again in a triangle ABD
`=> tan D = (AB)/(BC + CD)`
`=> tan 32^@ = h/(x + 100)`
`=> 0.6248 = h/(x + 100)`
`=> x + 100 = h/0.6248`
`=> 100 = h/0.6248 - h/1.9626`
`=> 100 = (h xx 1.9626 - h xx 0.6248)/(0.6248 xx 1.9626)`
`=> 100 = (h(1.9626 - 0.6248))/(0.6248 xx 1.9626)`
`=> 100 = (h(1.3378))/(0.6248 xx 1.9626)`
=> 100 x 0.6248 x 1.9626 = h x 1.3378
`=> h = (100 xx 0.6248 xx 1.9626)/1.3378`
`=> 122.6232/1.3378`
=> 91.66
`=> x = 91.66/1.9626`
= 46.7
So distance of the first position from the tower is = 100 + 46.7 = 146.7 m
Hence the height of tower 91.66 m and the desires distance is 146.7 m
APPEARS IN
संबंधित प्रश्न
The angle of elevation of a stationary cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45°. What is the height of the cloud above the lake level? (Use tan 15° = 0.268)
The angle of elevation on the top of a building from the foot of a tower is 30° . The angle of elevation of the top of the tower when seen from the top of the second water is 60° .If the tower is 60m high, find the height of the building.
The angle of elevation of the top of a tower from ta point on the same level as the foot of the tower is 30° . On advancing 150 m towards foot of the tower, the angle of elevation becomes 60° Show that the height of the tower is 129.9 metres.
A ladder 15 m long makes an angle of 60° with the wall. Find the height of the point where the ladder touches the wall.
The angles of elevation and depression of the top and bottom of a light-house from the top of a 60 m high building are 30° and 60° respectively. Find (i) the difference between the heights of the light-house and the building. (ii) the distance between the light-house and the building.
If the angle of elevation of a tower from a distance of 100 metres from its foot is 60°, then the height of the tower is
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between B and C. (tan 20° = 0.3640, `sqrt3` = 1.732)

A TV tower stands vertically on a bank of a canal, with a height of `10 sqrt3` m. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the distance between the opposite bank of the canal and the point with a 30° angle of elevation.
An electrician has to repair an electric fault on a pole of height 4 m. He needs to reach a point 1.3 m below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use which when inclined at an angle of 60° to the horizontal would enable him to reach the required position?
The angles of elevation of the bottom and the top of a flag fixed at the top of a 25 m high building are 30° and 60° respectively from a point on the ground. Find the height of the flag.
