Advertisements
Advertisements
प्रश्न
The angles of elevation and depression of the top and bottom of a light-house from the top of a 60 m high building are 30° and 60° respectively. Find (i) the difference between the heights of the light-house and the building. (ii) the distance between the light-house and the building.
उत्तर
Let AB be the building and CD be the light house.
Suppose the height of the light house be h m.
Given: AB = 60 m, ∠EAD = 30° and ∠CAE = 60°.
CE = AB = 60 m
∴ DE = CD − CE = (h − 60) m
In ΔEAD,
In ΔACE,
From (1) and (2), we get
∴ Difference between the height of light house and building = CD − AB = 80 m − 60 m = 20 m
Distance between the light house and building = BC = AE
APPEARS IN
संबंधित प्रश्न
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom circular ends are 20 cm and 12 cm, respectively. Find the height of the bucket and the area of metal sheet used in making the bucket. (use π = 3.14)
Two men are on opposite side of tower. They measure the angles of elevation of the top of the tower as 30 and 45 respectively. If the height of the tower is 50 meters, find the distance between the two men.
The angle of elevation on the top of a building from the foot of a tower is 30° . The angle of elevation of the top of the tower when seen from the top of the second water is 60° .If the tower is 60m high, find the height of the building.
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60° . At a point Y, 40m vertically above X, the angle of elevation is 45° . Find the height of tower PQ.
From the top of a hill, the angles of depression of two consecutive kilometer stones due east are found to be 45° and 30° respectivly. Find the height of the hill ?
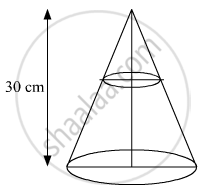
In fig. 9 is shown a right circular cone of height 30 cm. A small cone is cut off from the top by a plane parallel to the base. If the volume of the small cone is 127127 of the volume of cone, find at what height above the base is the section made.
The angle of elevation of the top of a tower at a point on the ground 50 m away from the foot of the tower is 45º. Then the height of the tower (in metres) is
A vertical pole of 30 m is fixed on a tower. From a point on the level ground, the angle of elevation of the top and bottom of the pole is 60° and 45°. Find the height of the tower.
From the top of an 8 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower. (Take `sqrt(3)` = 1.732).
The angle of elevation of the top of a 30 m high tower at a point 30 m away from the base of the tower is ______.
