Advertisements
Advertisements
Question
The angles of elevation and depression of the top and bottom of a light-house from the top of a 60 m high building are 30° and 60° respectively. Find (i) the difference between the heights of the light-house and the building. (ii) the distance between the light-house and the building.
Solution
Let AB be the building and CD be the light house.
Suppose the height of the light house be h m.
Given: AB = 60 m, ∠EAD = 30° and ∠CAE = 60°.
CE = AB = 60 m
∴ DE = CD − CE = (h − 60) m
In ΔEAD,
In ΔACE,
From (1) and (2), we get
∴ Difference between the height of light house and building = CD − AB = 80 m − 60 m = 20 m
Distance between the light house and building = BC = AE
APPEARS IN
RELATED QUESTIONS
A man standing on the deck of a ship, which is 8 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine the angle of elevation of the top of the tower from his eye.
From the point of a tower 100m high, a man observe two cars on the opposite sides to the tower with angles of depression 30° and 45 respectively. Find the distance between the cars
The angle of elevation on the top of a building from the foot of a tower is 30° . The angle of elevation of the top of the tower when seen from the top of the second water is 60° .If the tower is 60m high, find the height of the building.
The horizontal distance between two poles is 15 m. The angle of depression of the top of first pole as seen from the top of second pole is 30°. If the height of the second pole is 24 m, find the height of the first pole. Use`[sqrt3=1.732]`
From the top of a lighthouse, an observer looking at a ship makes angle of depression of 60°. If the height of the lighthouse is 90 metre, then find how far the ship is from the lighthouse.
From the top of the light house, an observer looks at a ship and finds the angle of depression to be 30°. If the height of the light-house is 100 meters, then find how far the ship is from the light-house.
The top of a 15 m high tower makes an angle of elevation of 60° with the bottom of an electronic pole and angle of elevation of 30° with the top of the pole. What is the height of the electric pole?
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is B to the North of A?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
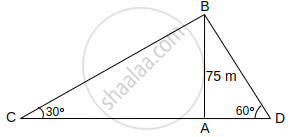
Two men on either side of a cliff 75 m high observe the angles of elevation of the top of the cliff to be 30° and 60°. Find the distance between the two men.