Advertisements
Advertisements
Question
From the point of a tower 100m high, a man observe two cars on the opposite sides to the tower with angles of depression 30° and 45 respectively. Find the distance between the cars
Solution
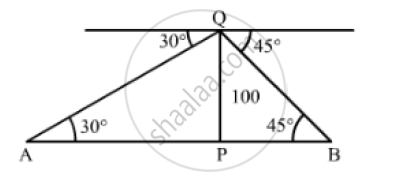
Let PQ be the tower
We have,
PQ = 100m, ∠PQR = 30° and ∠PBQ = 45°
In ΔAPQ,
`tan 30° = (PQ)/(AP)`
`⇒ 1/ sqrt(3) = 100/(AP)`
`⇒AP = 100 sqrt(3) m`
Also, in ΔBPQ,
` tan 45° = (PQ)/(BP)`
`⇒ 1 = 100/(BP)`
⇒ BP = 100M
Now , AB = AP+ BP
`= 100 sqrt(3) + 100`
`= 100( sqrt(3) +1)`
`= 100 xx (1.73 +1 )`
` = 100 xx 2.73`
= 273 m
So, the distance between the cars is 273m.
APPEARS IN
RELATED QUESTIONS
A man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of a hill as 30°. Find the distance of the hill from the ship and the height of the hill
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30º and that of the top of the flagstaff is 45º. Find the height of the tower.
A tower is 100√3 metres high. Find the angle of elevation of its top from a point 100 metres away from its foot.
From the top of a tower, 100, high, a man observes two cars on the opposite sides of the tower and in same straight line with its base, with angles of depression 30° and 45°. Find the distance between the cars. [Take `sqrt3` = 1.732]
The angle of elevation of the top of a chimney form the foot of a tower is 60° and the angle of depression of the foot of the chimney from the top of the tower is 30° . If the height of the tower is 40 meters. Find the height of the chimney.
A TV tower stands vertically on a bank of a canal, with a height of `10 sqrt3` m. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the distance between the opposite bank of the canal and the point with a 30° angle of elevation.
The angles of elevation of the top of a tower from two points distant s and t from its foot are complementary. Then the height of the tower is ____________.
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun is also increasing.
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top remains unchanged.
The angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is `sqrt(st)`
