Advertisements
Advertisements
Question
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun is also increasing.
Options
True
False
Solution
This statement is False.
Explanation:
To understand the fact of this question, consider the following example
I. A tower `2sqrt(3)` m high casts a shadow 2 m long on the ground, then the Sun’s elevation is 60°.
In ΔACB,
tan θ = `"AB"/"BC" = (2sqrt(3))/2`
⇒ tan θ = `sqrt(3)` = tan 60°
∴ θ = 60°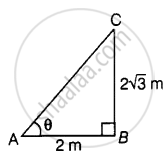
II. A same height of tower casts a shadow 4m more from preceding point, then the Sun’s elevation is 30°.
In ΔAPB,
tan θ = `"AB"/"PB" = "AB"/("PC" + "CB")`
⇒ tan θ = `(2sqrt(3))/(4 + 2) = (2sqrt(3))/6`
⇒ tan θ = `sqrt(3)/3 * sqrt(3)/sqrt(3) = 3/(3sqrt(3)`
⇒ tan θ = `1/sqrt(3)` = tan 30°
∴ θ = 30°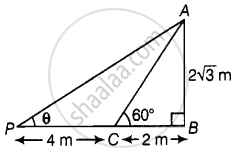
Hence, we conclude from above two examples that if the length of the shadow of a tower is increasing, then the angle of elevation of the Sun is decreasing.
APPEARS IN
RELATED QUESTIONS
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground, making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Two poles of equal heights are standing opposite each other an either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30º, respectively. Find the height of poles and the distance of the point from the poles.
Two points A and B are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are 60° and 45° respectively. If the height of the tower is 15 m, then find the distance between the points.
An electric pole is 10 m high. A steel wire tied to the top of the pole is affixed at a point on the ground to keep the pole upright. If the wire makes an angle of 45° with the horizontal through the foot of the pole, find the length of the wire.
A straight highway leads to the foot of a tower of height 50 m. From the top of the tower, the angles of depression of two cars standing on the highway are 30° and 60° respectively. What is the distance the two cars and how far is each car from the tower?
An observer 1.5m tall is 30 away from a chimney. The angle of elevation of the top of the chimney from his eye is 60 . Find the height of the chimney.
The ratio of the length of a rod and its shadow is `1 : sqrt3`. The angle of elevation of the sum is
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the North of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively. If the distance between the ships is `200[(sqrt(3) + 1)/sqrt(3)]` metres, find the height of the lighthouse.
A pole of height 30 m is observed from a point. The angle of depression of the point is 30°. Find the distance of the point from the base of the pole.
