Advertisements
Advertisements
Question
If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.
Options
True
False
Solution
This statement is False.
Explanation:
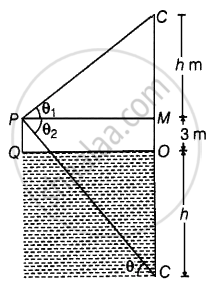
From figure, we observe that, a man standing on a platform at point P, 3 m above the surface of a lake observes a cloud at point C.
Let the height of the cloud from the surface of the platform is h and angle of elevation of the cloud is θ1.
Now at same point P a man observes a cloud reflection in the lake at this time the height of reflection of cloud in lake is (h + 3) because in lake platform height is also added to reflection of cloud.
So, angle of depression is different in the lake from the angle of elevation of the cloud above the surface of a lake
In ΔMPC,
tan θ1 = `"CM"/"PM" = "h"/"PM"`
⇒ `(tan θ_1)/"h" = 1/"PM"` ...(i)
In ΔCPM,
tan θ2 = `"CM"/"PM"`
= `("OC" + "OM")/"PM"`
= `("h" + 3)/"PM"`
⇒ `(tan θ_2)/("h" + 3) = 1/"PM"` ...(ii)
From equations (i) and (ii),
`(tan θ_1)/"h" = (tan θ_2)/("h" + 3)`
⇒ tan θ2 = `(("h" + 3)/"h") tan θ_1`
Hence, θ1 ≠ θ2
APPEARS IN
RELATED QUESTIONS
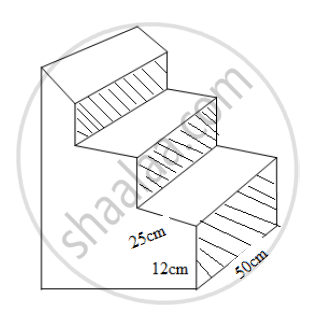
There are three stair-steps as shown in the figure below. Each stair step has width 25 cm, height 12 cm and length 50 cm. How many bricks have been used in it, if each brick is 12.5 cm x 6.25 cm x 4 cm?
The angle of elevation of an aeroplane from point A on the ground is 60˚. After flight of 15 seconds, the angle of elevation changes to 30˚. If the aeroplane is flying at a constant height of 1500√3 m, find the speed of the plane in km/hr.
On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects.
A TV tower stands vertically on a bank of a river/canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From a point 20 m away this point on the same bank, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the river/canal.
A solid right-circular cone of height 60 cm and radius 30 cm is dropped in a right-circular cylinder full of water of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder, in cubic metres ?
From the top of a lighthouse, the angle of depression of two ships on the opposite sides of it is observed to be 30° and 60°. If the height of the lighthouse is h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance between the ships is `(4"h")/sqrt(3)` m
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is B to the North of A?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
If at some time, the length of the shadow of a tower is `sqrt3` times its height, then the angle of elevation of the sun, at that time is ____________.
The angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is `sqrt(st)`
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Find the height of the tower.
