Advertisements
Advertisements
प्रश्न
If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.
विकल्प
True
False
उत्तर
This statement is False.
Explanation:
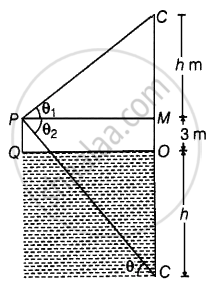
From figure, we observe that, a man standing on a platform at point P, 3 m above the surface of a lake observes a cloud at point C.
Let the height of the cloud from the surface of the platform is h and angle of elevation of the cloud is θ1.
Now at same point P a man observes a cloud reflection in the lake at this time the height of reflection of cloud in lake is (h + 3) because in lake platform height is also added to reflection of cloud.
So, angle of depression is different in the lake from the angle of elevation of the cloud above the surface of a lake
In ΔMPC,
tan θ1 = `"CM"/"PM" = "h"/"PM"`
⇒ `(tan θ_1)/"h" = 1/"PM"` ...(i)
In ΔCPM,
tan θ2 = `"CM"/"PM"`
= `("OC" + "OM")/"PM"`
= `("h" + 3)/"PM"`
⇒ `(tan θ_2)/("h" + 3) = 1/"PM"` ...(ii)
From equations (i) and (ii),
`(tan θ_1)/"h" = (tan θ_2)/("h" + 3)`
⇒ tan θ2 = `(("h" + 3)/"h") tan θ_1`
Hence, θ1 ≠ θ2
APPEARS IN
संबंधित प्रश्न
If the angle of elevation of cloud from a point 200 m above a lake is 30º and the angle of depression of its reflection in the lake is 60º, then find the height of the cloud above the lake
The angle of elevation of the top of an unfinished tower at a distance of 75m from its base is 30° .How much higher must the tower be raised so that the angle of elevation of its top at the same point may be 60 .
Two poles of equal heights are standing opposite to each other on either side of the road which is 80m wide, From a point P between them on the road, the angle of elevation of the top of one pole is 60 and the angle of depression from the top of another pole at P is 30 . Find the height of each pole and distance of the point P from the poles.
From the top of a lighthouse, an observer looking at a ship makes angle of depression of 60°. If the height of the lighthouse is 90 metre, then find how far the ship is from the lighthouse.
Two persons are a metres apart and the height of one is double that of the other. If from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary, then the height of the shorter post is
A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60ϒ and from the same point the angle of elevation of the top of the pedestal is 40ϒ. Find the height of the pedestal. (tan 40° = 0.8391, `sqrt(3)` = 1.732)
An aeroplane is flying parallel to the Earth’s surface at a speed of 175 m/sec and at a height of 600 m. The angle of elevation of the aeroplane from a point on the Earth’s surface is 37°. After what period of time does the angle of elevation increase to 53°? (tan 53° = 1.3270, tan 37° = 0.7536)
At some time of the day, the length of the shadow of a tower is equal to its height. Then, the sun’s altitude at that time is ______.
A Technician has to repair light on a pole of height 10 m. She needs to reach a point 1 m below the top of the pole to undertake the repair work. What should be the length of the ladder that she should use which, when inclined at an angle of 60∘ to the ground, would enable her to reach the required position? Also, how far from the foot of the pole should she place the foot of the ladder?
|
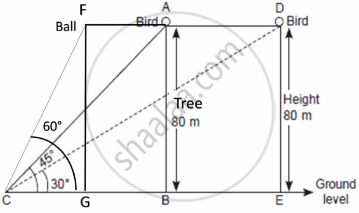
One evening, Kaushik was in a park. Children were playing cricket. Birds were singing on a nearby tree of height 80m. He observed a bird on the tree at an angle of elevation of 45°. When a sixer was hit, a ball flew through the tree frightening the bird to fly away. In 2 seconds, he observed the bird flying at the same height at an angle of elevation of 30° and the ball flying towards him at the same height at an angle of elevation of 60°.
|
- At what distance from the foot of the tree was he observing the bird sitting on the tree?
- How far did the bird fly in the mentioned time?
(or)
After hitting the tree, how far did the ball travel in the sky when Kaushik saw the ball? - What is the speed of the bird in m/min if it had flown `20(sqrt3 + 1) m`?