Advertisements
Advertisements
प्रश्न
From the top of a lighthouse, an observer looking at a ship makes angle of depression of 60°. If the height of the lighthouse is 90 metre, then find how far the ship is from the lighthouse.
उत्तर
Let AB be the lighthouse and C be the position of the ship from the lighthouse.
Suppose the distance of the ship from the lighthouse be x m.
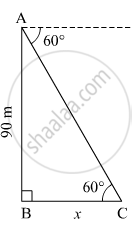
In right ∆ABC,
\[\tan60^\circ = \frac{AB}{BC}\]
\[ \Rightarrow \sqrt{3} = \frac{90}{x}\]
\[ \Rightarrow x = \frac{90}{\sqrt{3}} = 30\sqrt{3}\]
\[ \Rightarrow x = 30 \times 1 . 73 = 51 . 9 m\]
Thus, the ship is 51.9 m away from the lighthouse.
संबंधित प्रश्न
A passenger, while boarding the plane, slipped form the stairs and got hurt. The pilot took the passenger in the emergency clinic at the airport for treatment. Due to this, the plane got delayed by half an hour. To reach the destination 1500 km away in time, so that the passengers could catch the connecting flight, the speed of the plane was increased by 250 km/hour than the usual speed. Find the usual speed of the plane
What value is depicted in this question?
A 21 m deep well with diameter 6 m is dug and the earth from digging is evenly spread to form a platform 27 m ✕ 11 m. Find the height of the platform.[Use `pi=22/7`]
If a vertical pole 6m high has a shadow of length 2 √3 metres, find the angle of elevation of the sun.
From the top of a 15 m high building, the angle of elevation of the top of a tower is found to be 30°. From the bottom of the same building, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower and the distance between tower and the building.
The angles of depression of the top and bottom of 8 m tall building from the top of a multistoried building are 30° and 45° respectively. Find the height of the multistoried building and the distance between the two buildings.
A man sitting at a height of 20 m on a tall tree on a small island in the middle of a river observes two poles directly opposite to each other on the two banks of the river and in line with the foot of the tree. If the angles of depression of the feet of the poles from a point at which the man is sitting on the tree on either side of the river are 60° and 30°respectively. Find the width of the river.
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
An observer, 1.7 m tall, is 203–√203 m away from a tower. The angle of elevation from the of observer to the top of tower is 30°. Find the height of tower ?
If the angle of elevation of a tower from a distance of 100 metres from its foot is 60°, then the height of the tower is
If the angles of elevation of a tower from two points distant a and b (a>b) from its foot and in the same straight line from it are 30° and 60°, then the height of the tower is
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 84 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
The top of a 15 m high tower makes an angle of elevation of 60° with the bottom of an electronic pole and angle of elevation of 30° with the top of the pole. What is the height of the electric pole?
A lift in a building of height 90 feet with transparent glass walls is descending from the top of the building. At the top of the building, the angle of depression to a fountain in the garden is 60°. Two minutes later, the angle of depression reduces to 30°. If the fountain is `30sqrt(3)` feet from the entrance of the lift, find the speed of the lift which is descending.
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is B to the North of A?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
The distance of point A(-5, 6) from the origin is ______.
In given figure, the value of CE is ____________.
A ladder 15 metres long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, find the height of the wall.
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
A straight highway leads to the foot of a tower. A man standing on the top of the 75 m high tower observes two cars at angles of depression of 30° and 60°, which are approaching the foot of the tower. If one car is exactly behind the other on the same side of the tower, find the distance between the two cars. (use `sqrt(3)` = 1.73)
