Question

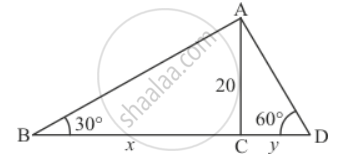
A man sitting at a height of 20 m on a tall tree on a small island in the middle of a river observes two poles directly opposite to each other on the two banks of the river and in line with the foot of the tree. If the angles of depression of the feet of the poles from a point at which the man is sitting on the tree on either side of the river are 60° and 30°respectively. Find the width of the river.

Answer 1

Let BC be the width of the river. And the angles of depression on either side of the river are 30° and 60° respectively. It is given that AC = 20 m.

 Let BC = x and CD = y. And ∠ABC = 30°, ∠ADC = 60°.

Here we have to find the width of the river.

We have the corresponding figure as follows

So we use trigonometric ratios.

In a triangle ABC

`=> tan B = (AC)/(BC)`

`=> tan 30^@ = 20/x`

`=> 1/sqrt3 = 20/x`

`=> x = 20sqrt3`

Again in a triangle ADC

`=> tan D = (AC)/(CD)`

`=> tan  60^@ = 20/y`

`=> sqrt3 = 20/y`

`=> y = 20/sqrt3`

`=> x + y = 20sqrt3 + 20/(20sqrt3)`

`=> x + y = 80/sqrt3`

Hence width of river is `80/sqrt3` m