Advertisements
Advertisements
Question
A man sitting at a height of 20 m on a tall tree on a small island in the middle of a river observes two poles directly opposite to each other on the two banks of the river and in line with the foot of the tree. If the angles of depression of the feet of the poles from a point at which the man is sitting on the tree on either side of the river are 60° and 30°respectively. Find the width of the river.
Solution
Let BC be the width of the river. And the angles of depression on either side of the river are 30° and 60° respectively. It is given that AC = 20 m.
Let BC = x and CD = y. And ∠ABC = 30°, ∠ADC = 60°.
Here we have to find the width of the river.
We have the corresponding figure as follows
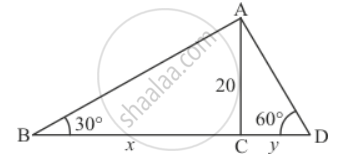
So we use trigonometric ratios.
In a triangle ABC
`=> tan B = (AC)/(BC)`
`=> tan 30^@ = 20/x`
`=> 1/sqrt3 = 20/x`
`=> x = 20sqrt3`
Again in a triangle ADC
`=> tan D = (AC)/(CD)`
`=> tan 60^@ = 20/y`
`=> sqrt3 = 20/y`
`=> y = 20/sqrt3`
`=> x + y = 20sqrt3 + 20/(20sqrt3)`
`=> x + y = 80/sqrt3`
Hence width of river is `80/sqrt3` m
APPEARS IN
RELATED QUESTIONS
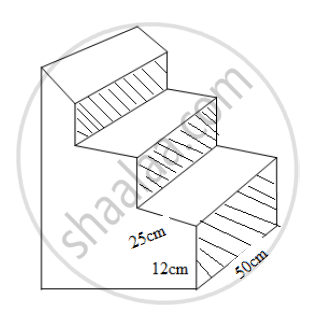
There are three stair-steps as shown in the figure below. Each stair step has width 25 cm, height 12 cm and length 50 cm. How many bricks have been used in it, if each brick is 12.5 cm x 6.25 cm x 4 cm?
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom circular ends are 20 cm and 12 cm, respectively. Find the height of the bucket and the area of metal sheet used in making the bucket. (use π = 3.14)
If the elevation of the sun changed from 30º to 60º, then find the difference between the lengths of shadows of a pole 15 m high, made at these two positions
From the top of the light house, an observer looks at a ship and finds the angle of depression to be 30°. If the height of the light-house is 100 meters, then find how far the ship is from the light-house.
The ratio of the length of a rod and its shadow is `1 : sqrt3`. The angle of elevation of the sum is
The height of the vertical pole is \[\sqrt{3}\] times the length of its shadow on the ground, then angle of elevation of the sun at that time is
When an observer at a distance of 12 m from a tree looks at the top of the tree, the angle of elevation is 60°. What is the height of the tree? `(sqrt 3 = 1.73)`
A flag pole ‘h’ metres is on the top of the hemispherical dome of radius ‘r’ metres. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30°. Find radius of the dome `(sqrt(3) = 1.732)`
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point, 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
In the given figure, AB is tower of height 50 m. A man standing on its top, observes two car on the opposite sides of the tower with angles of depression 30° and 45° respectively. Find the distance between the two cars.

