Advertisements
Advertisements
Question
Two poles of equal heights are standing opposite each other an either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30º, respectively. Find the height of poles and the distance of the point from the poles.
Solution 1
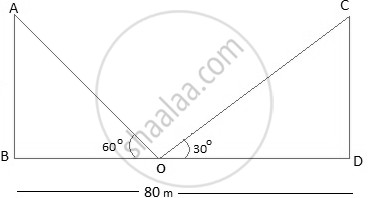
Let AB and CD be the poles and O is the point from where the elevation angles are measured.
In ΔABO
`("AB")/("BO") = tan 60°`
`("AB")/("BO") = sqrt3`
`"BO" = ("AB")/sqrt3`
In ΔCDO,
`("CD")/("DO") = tan 30°`
`("CD")/(80-"BO") = 1/sqrt3`
`"CD"sqrt3 = 80 - "BO"`
`"CD"sqrt3 = 80 - ("AB")/sqrt3`
`"CD"sqrt3+ ("AB")/sqrt3 = 80`
Since the poles are of equal heights,
CD = AB
`"CD"[sqrt3 + 1/sqrt3] = 80`
`"CD"((3+1)/sqrt3) = 80`
`"CD" = 20sqrt3`
`"BO"= ("AB")/sqrt3 = ("CD")/sqrt3`
= `((20sqrt3)/sqrt3)`m
= 20 m
DO = BD − BO
= (80 − 20) m
= 60 m
Therefore, the height of poles is `20sqrt3` and the point is 20 m and 60 m far from these poles.
Solution 2
Let AB and CD be the two poles of equal height.
O be the point makes an angle of elevation from the top of the poles of 60° and 30°, respectively.
Let OA = 80 - x, OD = x.
And ∠BOA = 30°, ∠COD = 60°.
Here, we have to find the height of the poles and the distance of the points from the poles.
We have the corresponding figure as follows:.
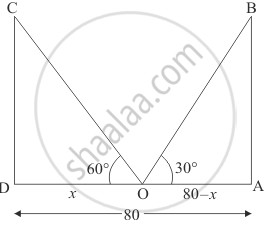
So we use trigonometric ratios.
In a triangle COD,
⇒ tan 60° = `"CD"/"DO"`
⇒ `sqrt(3) = "h"/"x"`
⇒ `"x" = "h"/sqrt(3)`
Again in a triangle AOB,
⇒ tan 30° = `"AB"/"OA"`
⇒ `(1)/sqrt(3) = "h"/(80 -"x")`
⇒ `sqrt(3)"h" = 80 - "x"`
⇒ `sqrt(3)"h" = 80 - "h"/sqrt(3)`
⇒ `sqrt(3)"h" + "h"/sqrt(3) = 80`
⇒ `3"h" + "h" = 80sqrt(3)`
⇒ `4"h" = 80sqrt(3)`
⇒ `"h" = 20sqrt(3)`
⇒ `"x" = (20sqrt(3))/sqrt(3)`
⇒ x = 20
And
⇒ OA = 80 - x
⇒ OA = 80 - 20
⇒ OA = 60
Hence, the height of pole is `20sqrt(3)` and distances are 20m, 60m respectively.
APPEARS IN
RELATED QUESTIONS
The angles of depression of the top and bottom of a 50 m high building from the top of a tower are 45° and 60° respectively. Find the height of the tower and the horizontal distance between the tower and the building (use `sqrt3`=1.73)
A balloon of radius γ makes an angle α at the eye of an observer and the angle of elevation of its centre is β. Then find the height of its centre from the ground level
A man on a cliff observes a fishing trawler at an angle of depression of 30º which is approaching the shore to the point immediately beneath the observer with a uniform speed. 6 minutes later, the angle of depression of the trawler is found to be 60º. Caliculate the time taken by the trawler to reach the shore
From a point on the ground 40 m away from the foot of a tower, the angle of elevation of the top of the tower is 30º. The angle of elevation of the top of a water tank (on the top of the tower) is 45º. Find the (i) height of the tower (ii) the depth of the tank.
The elevation of a tower at a station A due north of it is α and at a station B due west of A is β. Prove that the height of the tower is `\frac{AB\sin \alpha \sin \beta }{\sqrt{\sin^{2}\alpha -\sin ^{2}\beta `
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.

An electric pole is 10 m high. A steel wire tied to the top of the pole is affixed at a point on the ground to keep the pole upright. If the wire makes an angle of 45° with the horizontal through the foot of the pole, find the length of the wire.
The angle of elevation of the top of a tower from a point A on the ground is 30°. Moving a distance of 20metres towards the foot of the tower to a point B the angle of elevation increases to 60°. Find the height of the tower & the distance of the tower from the point A.
The angles of depression of the top and bottom of 8 m tall building from the top of a multistoried building are 30° and 45° respectively. Find the height of the multistoried building and the distance between the two buildings.
The angle of elevation of a stationary cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45°. What is the height of the cloud above the lake level? (Use tan 15° = 0.268)
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45 . If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60 , then find the height of the flagstaff [Use `sqrt(3)` 1.732]
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60° . At a point Y, 40m vertically above X, the angle of elevation is 45° . Find the height of tower PQ.
The shadow of a tower at a time is three times as long as its shadow when the angle of elevation of the sun is 60°. Find the angle of elevation of the sun at the time of the longer shadow ?
If the angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower in the same straight line with it are complementary, find the height of the tower.
The angle of elevation of the top of a cell phone tower from the foot of a high apartment is 60° and the angle of depression of the foot of the tower from the top of the apartment is 30°. If the height of the apartment is 50 m, find the height of the cell phone tower. According to radiation control norms, the minimum height of a cell phone tower should be 120 m. State if the height of the above mentioned cell phone tower meets the radiation norms
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between A and B. (tan 20° = 0.3640, `sqrt3` = 1.732)

At some time of the day, the length of the shadow of a tower is equal to its height. Then, the sun’s altitude at that time is ______.
A kite is flying at a height of 30 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.
From the top of building AB, a point C is observed on the ground whose angle of depression is 60° and which is at a distance of 40 m from the base of the building. Complete the following activity to find the height of building AB.

From figure, BC = `square`, ∠ACB = `square`
In ΔACB,
tan `square = square/(BC)`
⇒ `square = square/square`
⇒ `square = square`
Hence, the height of the building AB is `square`.
