Advertisements
Advertisements
Question
The angles of depression of the top and bottom of 8 m tall building from the top of a multistoried building are 30° and 45° respectively. Find the height of the multistoried building and the distance between the two buildings.
Solution
Let AD be the multistoried building of height hm. And the angle of depression of the top and bottom are 30° and 45°. We assume that BE = 8, CD = 8 and BC = x, ED = x and AC = h − 8. Here we have to find height and distance of the building.
We use trigonometric ratio.
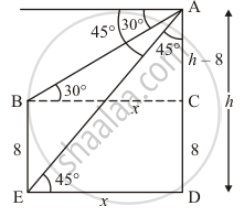
In ΔAED,
`=> tan E = (AD)/(DE)`
`=> tan 45^@= (AD)/(DE)`
`=> 1 = h/x`
=> x = h
Again in Δ ABC
`=> tan B = (AC)/(BC)`
`=> tan 30^@ = (h - 8)/x`
`=> 1/sqrt3 = (h - 8)/x`
`=> hsqrt3 - 8sqrt3 = x`
`> hsqrt3 - 8sqrt3 = h`
`=> h(sqrt3 - 1) = 8sqrt3`
`=> h = (8sqrt3)/(sqrt3 - 1) xx (sqrt3 + 1)/(sqrt3 + 1)`
`=> h = (24 + 8sqrt3)/2`
`=> h = (4(3 + sqrt3))`
And
`=> x = 4(3 + sqrt3)`
Hence the required height is `4(3 + sqrt3)` meter and distance is `4(3 + sqrt3)` meter
APPEARS IN
RELATED QUESTIONS
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45°. If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60°, then find the height of the flagstaff. [use √3=1.73]
From a point P on the ground the angle of elevation of the top of a tower is 30° and that of the top of a flag staff fixed on the top of the tower, is 60°. If the length of the flag staff is 5 m, find the height of the tower.
A person observed the angle of elevation of the top of a tower as 30°. He walked 50 m towards the foot of the tower along level ground and found the angle of elevation of the top of the tower as 60°. Find the height of the tower.
A parachutist is descending vertically and makes angles of elevation of 45° and 60° at two observing points 100 m apart from each other on the left side of himself. Find the maximum height from which he falls and the distance of the point where he falls on the ground form the just observation point.
The angle of elevation of a tower from a point on the same level as the foot of the tower is 30°. On advancing 150 metres towards the foot of the tower, the angle of elevation of the tower becomes 60°. Show that the height of the tower is 129.9 metres (Use `sqrt3 = 1.732`)
The vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height 6m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is
30 and that of the top of the flagstaff 60 . Find the height of the tower
[Use `sqrt(3)` 1.732 ]
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
If the altitude of the sum is at 60°, then the height of the vertical tower that will cast a shadow of length 30 m is
The length of the shadow of a tower standing on level ground is found to be 2x metres longer when the sun's elevation is 30°than when it was 45°. The height of the tower in metres is
The angle of elevation of a cloud from a point h metres above a lake is β. The angle of depression of its reflection in the lake is 45°. The height of location of the cloud from the lake is
