Advertisements
Advertisements
Question
The angle of elevation of a cloud from a point h metres above a lake is β. The angle of depression of its reflection in the lake is 45°. The height of location of the cloud from the lake is
Options
`("h"(1 + tan beta))/(1 - tan beta)`
`("h"(1 - tan beta))/(1 + tan beta)`
h tan(45° − β)
none of these
Solution
`("h"(1 + tan beta))/(1 - tan beta)`
Explanation;
Hint:
Consider the height of the cloud PC b x
PD = x − h
Let BC be y
In the right ΔADP, tan β = `"PD"/"AD"`
tan β = `(x - "h")/y`
⇒ y = `(x - "h")/(tan beta)` ...(1)
In the right ΔAQD, tan 45° = `"DQ"/"AD"`
1 = `(x + "h")/y`
⇒ y = x + h ...(2)
From (1) and (2) we get,
`(x - "h")/(tan beta)` = x + h
⇒ (x + h) tan β = x − h
⇒ x tan β + h tan β = x − h
h + h tan β = x − x tan β
⇒ h(1 + tan β) = x(1 − tan β)
x = `("h"(1 + tan beta))/((1 - tan beta))`
APPEARS IN
RELATED QUESTIONS
Two ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships as observed from the top of the light house are 60° and 45°. If the height of the light house is 200 m, find the distance between the two ships. [use √3=1.73]
The ratio of the height of a tower and the length of its shadow on the ground is `sqrt3 : 1`. What is the angle of elevation of the sun?
The Distance of the point (−3, 4) from the x-axis is
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is
The height of the vertical pole is \[\sqrt{3}\] times the length of its shadow on the ground, then angle of elevation of the sun at that time is
In given figure, the value of AE is ____________.
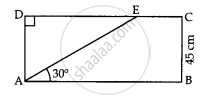
A vertical pole of 30 m is fixed on a tower. From a point on the level ground, the angle of elevation of the top and bottom of the pole is 60° and 45°. Find the height of the tower.
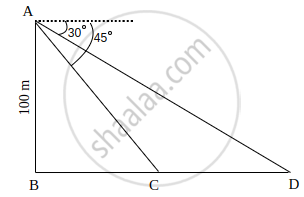
As observed from the top of a light house 100 m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° to 45°. Determine the distance travelled by the ship during this time. [Use `sqrt(3)` = 1.732]
Read the following passage:
|
Radio towers are used for transmitting a range of communication services including radio and television. The tower will either act as an antenna itself or support one or more antennas on its structure; On a similar concept, a radio station tower was built in two Sections A and B. Tower is supported by wires from a point O. Distance between the base of the tower and point O is 36 cm. From point O, the angle of elevation of the top of the Section B is 30° and the angle of elevation of the top of Section A is 45°.
|
Based on the above information, answer the following questions:
- Find the length of the wire from the point O to the top of Section B.
- Find the distance AB.
OR
Find the area of ∠OPB. - Find the height of the Section A from the base of the tower.

