Advertisements
Advertisements
Question
Read the following passage:
|
Radio towers are used for transmitting a range of communication services including radio and television. The tower will either act as an antenna itself or support one or more antennas on its structure; On a similar concept, a radio station tower was built in two Sections A and B. Tower is supported by wires from a point O. Distance between the base of the tower and point O is 36 cm. From point O, the angle of elevation of the top of the Section B is 30° and the angle of elevation of the top of Section A is 45°.
|
Based on the above information, answer the following questions:
- Find the length of the wire from the point O to the top of Section B.
- Find the distance AB.
OR
Find the area of ∠OPB. - Find the height of the Section A from the base of the tower.
Solution
i. Let the length of wire BO = x cm
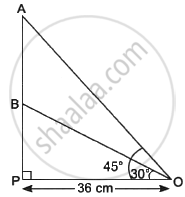
∴ cos 30° = `(PO)/(BO)`
`\implies sqrt(3)/2 = 36/x`
`\implies` x = `(36 xx 2)/sqrt(3) xx sqrt(3)/sqrt(3)`
= `12 xx 2sqrt(3)`
= `24sqrt(3)` cm
ii. In ΔAPO, tan 45° = `(AP)/(PO)`
`\implies` 1 = `(AP)/36`
`\implies` AP = 36 cm ...(1)
Now, In ΔPBO,
tan 30° = `(BP)/(PO)`
`\implies 1/sqrt(3) = (BP)/36`
`\implies` BP = `36/sqrt(3) xx sqrt(3)/sqrt(3)`
= `36/3 sqrt(3)`
= `12sqrt(3)` cm
∴ AB = AP – BP
= `36 - 12sqrt(3)` cm
OR
In ΔOPB
tan 30° = `(BP)/(PO)`
`\implies 1/sqrt(3) = (BP)/36`
BP = `36/sqrt(3)`
= `36/sqrt(3) xx sqrt(3)/sqrt(3)`
= `12sqrt(3)` cm
Now, Area of ΔOPB = `1/2 xx "height" xx "base"`
= `1/2 xx BP xx OP`
= `1/2 xx 12sqrt(3) xx 36`
= `216sqrt(3)` cm2
iii. In ΔAPO, tan 45° = `(AP)/36`
1 = `(AP)/36`
A = 36 cm
Height of section A from the base of the tower = AP = 36 cm
APPEARS IN
RELATED QUESTIONS
As observed from the top of a 100 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships. [Use `sqrt3` = 1.732]
An observer 1.5m tall is 30 away from a chimney. The angle of elevation of the top of the chimney from his eye is 60 . Find the height of the chimney.
Two buildings are in front of each other on a road of width 15 meters. From the top of the first building, having a height of 12 meter, the angle of elevation of the top of the second building is 30°.What is the height of the second building?
While landing at an airport, a pilot made an angle of depression of 20°. Average speed of the plane was 200 km/hr. The plane reached the ground after 54 seconds. Find the height at which the plane was when it started landing. (sin 20° = 0.342)
From a point on the ground, 20 m away from the foot of a vertical tower, the angle elevation of the top of the tower is 60°, What is the height of the tower?
If a 1.5 m tall girl stands at a distance of 3 m from a lamp-post and casts a shadow of length 4.5 m on the ground, then the height of the lamp-post is
A ladder makes an angle of 60º with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is
From the top of a lighthouse, the angle of depression of two ships on the opposite sides of it is observed to be 30° and 60°. If the height of the lighthouse is h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance between the ships is `(4"h")/sqrt(3)` m
A tower is 60 m heigh. Its shadow is x metres shorter when the sun’s altitude is 45° than when it has been 30°, then x is equal to
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and also the height of the other tower.

