Question

Read the following passage:

Radio towers are used for transmitting a range of communication services including radio and television. The tower will either act as an antenna itself or support one or more antennas on its structure; On a similar concept, a radio station tower was built in two Sections A and B. Tower is supported by wires from a point O. Distance between the base of the tower and point O is 36 cm. From point O, the angle of elevation of the top of the Section B is 30° and the angle of elevation of the top of Section A is 45°.

Based on the above information, answer the following questions:

1. Find the length of the wire from the point O to the top of Section B. 
2. Find the distance AB.
   OR
   Find the area of ∠OPB.
3. Find the height of the Section A from the base of the tower.

Answer 1

i. Let the length of wire BO = x cm

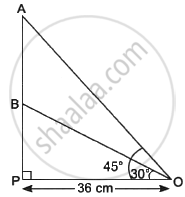
∴ cos 30° = `(PO)/(BO)`

`\implies sqrt(3)/2 = 36/x`

`\implies` x = `(36 xx 2)/sqrt(3) xx sqrt(3)/sqrt(3)`

= `12 xx 2sqrt(3)`

= `24sqrt(3)` cm

ii. In ΔAPO, tan 45° = `(AP)/(PO)`

`\implies` 1 = `(AP)/36`

`\implies` AP = 36 cm  ...(1)

Now, In ΔPBO,

tan 30° = `(BP)/(PO)`

`\implies 1/sqrt(3) = (BP)/36`

`\implies` BP = `36/sqrt(3) xx sqrt(3)/sqrt(3)`

= `36/3 sqrt(3)`

= `12sqrt(3)` cm

∴ AB = AP – BP

= `36 - 12sqrt(3)` cm

OR

In ΔOPB

tan 30° = `(BP)/(PO)`

`\implies 1/sqrt(3) = (BP)/36`

BP = `36/sqrt(3)`

= `36/sqrt(3) xx sqrt(3)/sqrt(3)`

= `12sqrt(3)` cm

Now, Area of ΔOPB = `1/2 xx "height" xx "base"`

= `1/2 xx BP xx OP`

= `1/2 xx 12sqrt(3) xx 36`

= `216sqrt(3)` cm²

iii. In ΔAPO, tan 45° = `(AP)/36`

1 = `(AP)/36`

A = 36 cm

Height of section A from the base of the tower = AP = 36 cm