Advertisements
Advertisements
प्रश्न
A flag-staff stands on the top of a 5 m high tower. From a point on the ground, the angle of elevation of the top of the flag-staff is 60° and from the same point, the angle of elevation of the top of the tower is 45°. Find the height of the flag-staff.
उत्तर
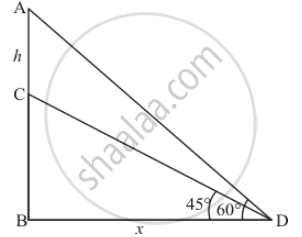
Let BC be the tower height of 5 m. flag height is hm and an angle of elevation of the top of the tower is 45° and an angle of elevation of the top of the flag is 60°.
Let AC = hm and BC = 5 m and ∠ADB = 60°, ∠CDB = 45°
We have the corresponding angle as follows
So we use trigonometric ratios.
In a triangle ΔBCD
`=> tan 44^@ = (BC)/(BD)`
`=> 1 = 5/x`
`=> x= 5`
Again in a triangle ABD
`=> tan 60^@ = (AB)/(BD)`
`=> sqrt3 = (5 + h)/5`
`=> h = 5(sqrt3 - 1)`
`=> h = 3.66`
Hence the height of flag is 3.66 m
APPEARS IN
संबंधित प्रश्न
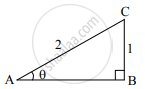
In the following figure, in ΔABC, BC = 1, AC = 2, ∠B = 90°. Find the value of sin θ.
From a point on the ground 40 m away from the foot of a tower, the angle of elevation of the top of the tower is 30º. The angle of elevation of the top of a water tank (on the top of the tower) is 45º. Find the (i) height of the tower (ii) the depth of the tank.
An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine the angle of elevation of the top of the tower from his eye.
From a point on the ground 40m away from the foot of a tower, the angle of elevation of the top of the tower is 30 . The angle of elevation of the top of a water tank (on the top of the tower) is 45 , Find (i) the height of the tower, (ii) the depth of the tank.
A storm broke a tree and the tree top rested on ground 20 m away from the
base of the tree, making an angle of 60o with the ground. Find the height
of the tree.
If the ratio of the height of a tower and the length of its shadow is `sqrt3:1`, what is the angle of elevation of the Sun?
From the top of a tree of height 13 m the angle of elevation and depression of the top and bottom of another tree are 45° and 30° respectively. Find the height of the second tree. `(sqrt(3) = 1.732)`
The electric pole subtends an angle of 30° at a point on the same level as its foot. At a second point ‘b’ metres above the first, the depression of the foot of the pole is 60°. The height of the pole (in metres) is equal to
The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 20 meters towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower ____________.
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun is also increasing.
