Advertisements
Advertisements
प्रश्न
From a point on the ground 40m away from the foot of a tower, the angle of elevation of the top of the tower is 30 . The angle of elevation of the top of a water tank (on the top of the tower) is 45 , Find (i) the height of the tower, (ii) the depth of the tank.
उत्तर
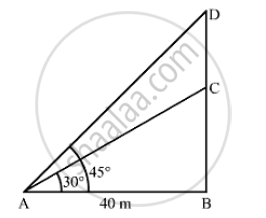
Let BC be the tower and CD be the water tank.
We have,
AB = 40m, ∠BAC = 30° and ∠BAD = 45°
In ΔABD,
` tan 45° = (BD)/(AB)`
`⇒ 1 = (BD)/40`
⇒ BD = 40 M
Now, in Δ ABC
`tan 30° = (BC)/(AB)`
`⇒1/ sqrt(3) = (BC) /40`
`⇒ BC = 40/sqrt(3)`
`⇒ BC = 40/ sqrt(3) xx sqrt(3)/sqrt(3)`
`⇒ BC = (40sqrt(3) )/3 m`
`"(i) The height of the tower," BC = (40 sqrt(3))/3 = (40 xx 1.73)/3 = 23.067 ~~ 23.1 m`
`"(ii) The depth of the tank " CD = (BD - BC) = (40-23.1 ) = 16.9 m`
APPEARS IN
संबंधित प्रश्न
There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on two banks, and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively 30º and 45º, find the height of the tree. (Use `sqrt(3)` = 1.732)
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
The angle of elevation of an aeroplane from a point on the ground is 45°. After a flight of 15 seconds, the elevation changes to 30°. If the aeroplane is flying at a height of 3000 metres, find the speed of the aeroplane.
A tower subtends an angle 𝛼 at a point A in the plane of its base and the angle if depression of the foot of the tower at a point b metres just above A is β. Prove that the height of the tower is b tan α cot β
An observer 1.5m tall is 30 away from a chimney. The angle of elevation of the top of the chimney from his eye is 60 . Find the height of the chimney.
A pole casts a shadow of length \[2\sqrt{3}\] m on the ground, when the sun's elevation is 60°. Find the height of the pole.
If two towers of heights h1 and h2 subtend angles of 60° and 30° respectively at the mid-point of the line joining their feet, then h1: h2 = ____________.
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top remains unchanged.
From the base of a pole of height 20 meter, the angle of elevation of the top of a tower is 60°. The pole subtends an angle 30° at the top of tower. Then the height of tower is ______.
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks, find the width of the river. (Use `sqrt(3)` = 1.73)
