English Medium
Academic Year: 2022-2023
Date & Time: 21st March 2023, 10:30 am
Duration: 3h
Advertisements
General Instructions:
- This question paper contains 38 questions.
All questions are compulsory. - This Question Paper is divided into FIVE Sections - Section A, B, C, D, and E.
- In Section - A question number 1 to 18 are Multiple Choice Questions (MCQs) and question number 19 & 20 are Assertion Reason based question of 1 mark each.
- In Section - B questions number 21 to 25 are Very Short-Answer-I (SA-I) type questions of 2 marks each.
- In Section - C questions number 26 to 31 are Short Answer-II (SA-II) type questions carrying 3 marks each.
- In Section - D questions number 32 to 35 are Long Answer (LA) type questions carrying 5 marks each.
- In Section - E questions number 36 to 38 are Case Study/Passage based integrated units and assessment questions carrying 4
marks each. Internal choice is provided in 2 marks question in each case-study. - There is no overall choice. However, an internal choice has been provided in 2 questions in Section - B, 2 questions in Section - C, 2 questions in Section - D, and 3 questions in Section - E.
- Draw neat figures wherever required. Take π = `22/7` wherever required if not stated.
- Use of calculator is NOT allowed.
If p2 = `32/50`, then p is a/an ______.
whole number
integer
rational number
irrational number
Chapter: [0.011000000000000001] Real Numbers
The distance of the point (–6, 8) from x-axis is ______.
6 units
– 6 units
8 units
10 units
Chapter: [0.031] Lines (In Two-dimensions) [0.031] Lines (In Two-dimensions)
The number of quadratic polynomials having zeroes –5 and –3 is ______.
1
2
3
more than 3
Chapter: [0.021] Polynomials
The point of intersection of the line represented by 3x – y = 3 and y-axis is given by ______.
(0, –3)
(0, 3)
(2, 0)
(–2, 0)
Chapter:
The circumferences of two circles are in the ratio 4 : 5. What is the ratio of their radii?
16 : 25
25 : 16
`2 : sqrt(5)`
4 : 5
Chapter: [0.061] Areas Related to Circles
The LCM of smallest 2-digit number and smallest composite number is ______.
12
4
20
40
Chapter: [0.011000000000000001] Real Numbers
The distance of the point (–4, 3) from y-axis is ______.
–4
4
3
5
Chapter: [0.031] Lines (In Two-dimensions) [0.031] Lines (In Two-dimensions)
If one zero of the quadratic polynomial x2 + 3x + k is 2, then the value of k is ______.
10
- 10
5
- 5
Chapter: [0.021] Polynomials
If the quadratic equation ax2 + bx + c = 0 has two real and equal roots, then 'c' is equal to ______.
`(-b)/(2a)`
`b/(2a)`
`(-b^2)/(4a)`
`b^2/(4a)`
Chapter: [0.023] Quadratic Equations
In the given figure, DE || BC. If AD = 3 cm, AB = 7 cm and EC = 3 cm, then the length of AE is ______.
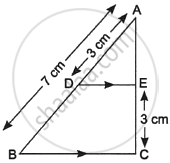
2 cm
2.25 cm
3.5 cm
4 cm
Chapter: [0.040999999999999995] Triangles
A bag contains 5 pink, 8 blue and 7 yellow balls. One ball is drawn at random from the bag. What is the probability of getting neither a blue nor a pink ball?
`1/4`
`2/5`
`7/20`
`13/20`
Chapter: [0.07200000000000001] Probability
The volume of a right circular cone whose area of the base is 156 cm2 and the vertical height is 8 cm, is ______.
2496 cm3
1248 cm3
1664 cm3
416 cm3
Chapter: [0.062] Surface Areas and Volumes
3 chairs and 1 table cost ₹ 900; whereas 5 chairs and 3 tables cost ₹ 2,100. If the cost of 1 chair is ₹ x and the cost of 1 table is ₹ y, then the situation can be represented algebraically as ______.
3x + y = 900, 3x + 5y = 2100
x + 3y = 900, 3x + 5y = 2100
3x + y = 900, 5x + 3y = 2100
x + 3y = 900, 5x + 3y = 2100
Chapter: [0.022000000000000002] Pair of Linear Equations in Two Variables
In the given figure, PA and PB are tangents from external point P to a circle with centre C and Q is any point on the circle. Then the measure of ∠AQB is ______.

`62 (1/2)^circ`
125°
55°
90°
Chapter: [0.042] Circles
A card is drawn at random from a well shuffled deck of 52 playing cards. The probability of getting a face card is ______.
`1/2`
`3/13`
`4/13`
`1/13`
Chapter: [0.07200000000000001] Probability
A box contains 90 discs, numbered from 1 to 90. If one disc is drawn at random from the box, the probability that it bears a prime number less than 23, is ______.
`7/90`
`9/90`
`1/9`
`10/90`
`4/15`
`4/45`
`8/89`
\[\frac{9}{89}\]
Chapter: [0.07200000000000001] Probability [0.07200000000000001] Probability
Advertisements
The coordinates of the point where the line 2y = 4x + 5 crosses x-axis is ______.
`(0, (-5)/4)`
`(0, 5/2)`
`((-5)/4, 0)`
`((-5)/2, 0)`
Chapter: [0.031] Lines (In Two-dimensions) [0.031] Lines (In Two-dimensions)
cos4 A − sin4 A is equal to ______.
2 cos2 A + 1
2 cos2 A − 1
2 sin2 A − 1
2 sin2 A + 1
Chapter: [0.051] Introduction to Trigonometry [0.052000000000000005] Trigonometric Identities
Statement A (Assertion): If 5 + `sqrt(7)` is a root of a quadratic equation with rational co-efficients, then its other root is 5 – `sqrt(7)`.
Statement R (Reason): Surd roots of a quadratic equation with rational co-efficients occur in conjugate pairs.
Both Assertion (A) and Reason (R) are true; and Reason (R) is the correct explanation of Assertion (A).
Both Assertion (A) and Reason (R) are true; but Reason (R) is not the correct explanation of Assertion (A).
Assertion (A) is true but Reason (R) is false.
Assertion (A) is false but Reason (R) is true.
Chapter: [0.023] Quadratic Equations
Statement A (Assertion): For 0 < θ ≤ 90°, cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other.
Statement R (Reason): cosec2 θ – cot2 θ = 1
Both Assertion (A) and Reason (R) are true; and Reason (R) is the correct explanation of Assertion (A).
Both Assertion (A) and Reason (R) are true; but Reason (R) is not the correct explanation of Assertion (A).
Assertion (A) is true but Reason (R) is false.
Assertion (A) is false but Reason (R) is true.
Chapter: [0.051] Introduction to Trigonometry
Show the 6n cannot end with digit 0 for any natural number 'n'.
Chapter: [0.011000000000000001] Real Numbers
Find the HCF and LCM of 72 and 120.
Chapter: [0.011000000000000001] Real Numbers
A line intersects y-axis and x-axis at point P and Q, respectively. If R(2, 5) is the mid-point of line segment PQ, them find the coordinates of P and Q.
Chapter: [0.031] Lines (In Two-dimensions)
Find the length of the shadow on the ground of a pole of height 18m when angle of elevation θ of the sun is such that tan θ = `6/7`.
Chapter: [0.053] Some Applications of Trigonometry
Find the points on the x-axis, each of which is at a distance of 10 units from the point A(11, –8).
Chapter: [0.031] Lines (In Two-dimensions) [0.031] Lines (In Two-dimensions)
In the given figure, ABC is a triangle in which DE||BC. If AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, then find the value of x.
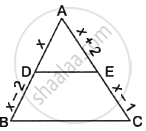
Chapter: [0.040999999999999995] Triangles
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using similarity criterion for two triangles, show that `"OA"/"OC"="OB"/"OD"`.
Chapter: [0.040999999999999995] Triangles
In the given figure, AB and CD are diameters of a circle with centre O perpendicular to each other. If OA = 7 cm, find the area of shaded region.
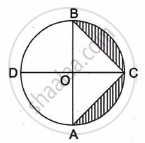
Chapter: [0.061] Areas Related to Circles
If sin θ + cos θ = p and sec θ + cosec θ = q, then prove that q(p2 – 1) = 2p.
Chapter: [0.051] Introduction to Trigonometry [0.052000000000000005] Trigonometric Identities
In the following figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ΔABD ∼ ΔECF.
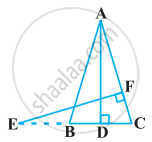
Chapter: [0.040999999999999995] Triangles
Advertisements
The sum of two natural numbers is 15 and the sum of their reciprocals is `3/10`. Find the numbers.
Chapter: [0.023] Quadratic Equations
If α and β are roots of the quadratic equation x2 – 7x + 10 = 0, find the quadratic equation whose roots are α2 and β2.
Chapter: [0.023] Quadratic Equations
Proved that `(1 + secA)/secA = (sin^2A)/(1 - cos A)`.
Chapter: [0.051] Introduction to Trigonometry [0.052000000000000005] Trigonometric Identities
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the sector formed by the arc. (Use π = `22/7`)
Chapter: [0.061] Areas Related to Circles
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the length of the arc. (Use π = `22/7`)
Chapter: [0.061] Areas Related to Circles
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ.
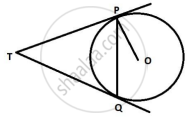
Chapter: [0.042] Circles
A circle touches the side BC of a ΔABC at a point P and touches AB and AC when produced at Q and R respectively. As shown in the figure that AQ = `1/2` (Perimeter of ΔABC).

Chapter: [0.042] Circles
A solid is in the shape of a right-circular cone surmounted on a hemisphere, the radius of each of them being 7 cm and the height of the cone is equal to its diameter. Find the volume of the solid.
Chapter: [0.062] Surface Areas and Volumes
A solid is in the shape of a cone surmounted on a hemisphere, the radius of each of them being 3.5 cm and the total height of the solid is 9.5 cm. Find the volume of the solid.
Chapter: [0.062] Surface Areas and Volumes
Find the sum of the integers between 100 and 200 that are
- divisible by 9
- not divisible by 9
[Hint (ii) : These numbers will be : Total numbers – Total numbers divisible by 9]
Chapter: [0.024] Arithmetic Progressions
Find the sum of the integers between 100 and 200 that are not divisible by 9.
Chapter: [0.024] Arithmetic Progressions
Solve the equation:
– 4 + (–1) + 2 + 5 + ... + x = 437
Chapter: [0.024] Arithmetic Progressions
Read the following passage:
|
A coaching institute of Mathematics conducts classes in two batches I and II and fees for rich and poor children are different. In batch I, there are 20 poor and 5 rich children, whereas in batch II, there are 5 poor and 25 rich children. The total monthly collection of fees from batch I is ₹9,000 and from batch II is ₹26,000. Assume that each poor child pays ₹x per month and each rich child pays ₹y per month.
|
Based on the above information, answer the following questions:
- Represent the information given above in terms of x and y.
- Find the monthly fee paid by a poor child.
OR
Find the difference in the monthly fee paid by a poor child and a rich child. - If there are 10 poor and 20 rich children in batch II, what is the total monthly collection of fees from batch II?
Chapter: [0.022000000000000002] Pair of Linear Equations in Two Variables
Read the following passage:
|
Radio towers are used for transmitting a range of communication services including radio and television. The tower will either act as an antenna itself or support one or more antennas on its structure; On a similar concept, a radio station tower was built in two Sections A and B. Tower is supported by wires from a point O. Distance between the base of the tower and point O is 36 cm. From point O, the angle of elevation of the top of the Section B is 30° and the angle of elevation of the top of Section A is 45°.
|
Based on the above information, answer the following questions:
- Find the length of the wire from the point O to the top of Section B.
- Find the distance AB.
OR
Find the area of ∠OPB. - Find the height of the Section A from the base of the tower.
Chapter: [0.053] Some Applications of Trigonometry
Read the following passage:
|
"Eight Ball" is a game played on a pool table with 15 balls numbered 1 to 15 and a "cue ball" that is solid and white. Of the 15 numbered balls, eight are solid (non-white) coloured and numbered 1 to 8 and seven are striped balls numbered 9 to 15.
|
Based on the above information, answer the following questions:
- What is the probability that the drawn ball bears number 8?
- What is the probability that the drawn ball bears an even number?
OR
What is the probability that the drawn ball bears a number, which is a multiple of 3? - What is the probability that the drawn ball is a solid coloured and bears an even number?
Chapter: [0.07200000000000001] Probability
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
CBSE previous year question papers Class 10 Mathematics with solutions 2022 - 2023
Previous year Question paper for CBSE Class 10 Maths-2023 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of CBSE Class 10.
How CBSE Class 10 Question Paper solutions Help Students ?
• Question paper solutions for Mathematics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.



