Advertisements
Advertisements
Question
A line intersects y-axis and x-axis at point P and Q, respectively. If R(2, 5) is the mid-point of line segment PQ, them find the coordinates of P and Q.
Solution
Let P point be (0, y)
and Q point be (x, 0)
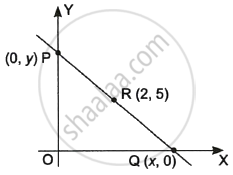
Since, on y-axis, x = 0 and on x-axis, y = 0
Let coordinates of point P be (0, y)
and coordinates of point Q be (x, 0)
Since, mid-point of points (x1, y1) and (x2, y2) is
`((x_1 + x_2)/2, (y_1 + y_2)/2)`
∴ 2 = `(0 + x)/2 \implies` x = 4
and 5 = `(y + 0)/2 \implies` y = 10
∴ coordinates of P = (0, 10)
and coordinates of Q = (4, 0)
APPEARS IN
RELATED QUESTIONS
Let P and Q be the points of trisection of the line segment joining the points A(2, -2) and B(-7, 4) such that P is nearer to A. Find the coordinates of P and Q.
If A(–2, –1), B(a, 0), C(4, b) and D(1, 2) are the vertices of a parallelogram, find the values of a and b
Three vertices of a parallelogram are (a+b, a-b), (2a+b, 2a-b), (a-b, a+b). Find the fourth vertex.
If two vertices of a parallelogram are (3, 2) (-1, 0) and the diagonals cut at (2, -5), find the other vertices of the parallelogram.
In what ratio does the point (a, 6) divide the join of (–4, 3) and (2, 8)? Also, find the value of a.
Points A, B, C and D divide the line segment joining the point (5, –10) and the origin in five equal parts. Find the co-ordinates of B and D.
In the given figure, line APB meets the x-axis at point A and y-axis at point B. P is the point (−4, 2) and AP : PB = 1 : 2. Find the co-ordinates of A and B.
Find the ratio in which the line segment joining A (2, -3) and B(S, 6) i~ divided by the x-axis.
The vertices of a parallelogram in order are A(1, 2), B(4, y), C(x, 6) and D(3, 5). Then (x, y) is ______.
The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC. What are the coordinates of the centroid of the triangle ABC?
