Advertisements
Advertisements
प्रश्न
A line intersects y-axis and x-axis at point P and Q, respectively. If R(2, 5) is the mid-point of line segment PQ, them find the coordinates of P and Q.
उत्तर
Let P point be (0, y)
and Q point be (x, 0)
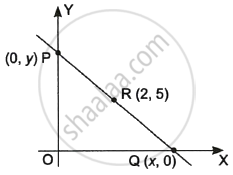
Since, on y-axis, x = 0 and on x-axis, y = 0
Let coordinates of point P be (0, y)
and coordinates of point Q be (x, 0)
Since, mid-point of points (x1, y1) and (x2, y2) is
`((x_1 + x_2)/2, (y_1 + y_2)/2)`
∴ 2 = `(0 + x)/2 \implies` x = 4
and 5 = `(y + 0)/2 \implies` y = 10
∴ coordinates of P = (0, 10)
and coordinates of Q = (4, 0)
APPEARS IN
संबंधित प्रश्न
Find the coordinates of points which trisect the line segment joining (1, –2) and (–3, 4)
Prove that the points (–2, –1), (1, 0), (4, 3) and (1, 2) are the vertices of a parallelogram. Is it a rectangle ?
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Find the coordinates of the points which divide the line segment joining A (−2, 2) and B (2, 8) into four equal parts.
Find the area of a rhombus if its vertices are (3, 0), (4, 5), (− 1, 4) and (− 2, −1) taken in order.
[Hint: Area of a rhombus = `1/2` (product of its diagonals)]
Find the lengths of the medians of a triangle whose vertices are A (−1,3), B(1,−1) and C(5, 1).
Find the length of the medians of a ΔABC having vertices at A(0, -1), B(2, 1) and C(0, 3).
Points A, B, C and D divide the line segment joining the point (5, –10) and the origin in five equal parts. Find the co-ordinates of B and D.
If the point C (–1, 2) divides internally the line-segment joining the points A (2, 5) and B (x, y) in the ratio 3 : 4, find the value of x2 + y2 ?
The origin o (0, O), P (-6, 9) and Q (12, -3) are vertices of triangle OPQ. Point M divides OP in the ratio 1: 2 and point N divides OQ in the ratio 1: 2. Find the coordinates of points M and N. Also, show that 3MN = PQ.
