Advertisements
Advertisements
प्रश्न
The origin o (0, O), P (-6, 9) and Q (12, -3) are vertices of triangle OPQ. Point M divides OP in the ratio 1: 2 and point N divides OQ in the ratio 1: 2. Find the coordinates of points M and N. Also, show that 3MN = PQ.
उत्तर
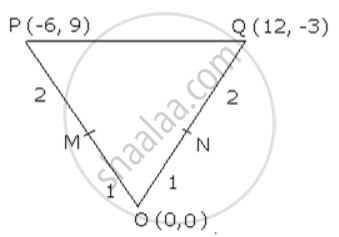
It is given that M divides OP in the ratio 1: 2 and point N divides OQ in the ratio 1: 2.
Using section formula, the coordinates of M are
`((-6 + 0)/ 3 , (9 + 0)/3) = (-2 , 3)`
Using section formula, the coordinates of N are
`((12 + 0)/3 , (-3 + 0)/3) = (4 , -1)`
Thus, the ooordinates of M and N are ( -2, 3) and ( 4, -1) respectively.
Now, using distance formula, we have:
PQ = `sqrt ((-6 -12)^2 + (9 + 3)^2) = sqrt (324 + 144) = sqrt 468`
MN = `sqrt ((4 + 2)^2 + (-1-3)^2) = sqrt (36 + 36) = sqrt 52`
It can be observed that :
PQ = `sqrt 468 = sqrt (9 xx 52) = 3 sqrt 52 = 3 "MN"`
Hence proved.
APPEARS IN
संबंधित प्रश्न
Find the coordinates of the centroid of a triangle whose vertices are (–1, 0), (5, –2) and (8, 2)
Find the ratio in which the line segment joining A (1, −5) and B (−4, 5) is divided by the x-axis. Also, find the coordinates of the point of division.
Given a line segment AB joining the points A(−4, 6) and B(8, −3). Find:
- the ratio in which AB is divided by the y-axis.
- find the coordinates of the point of intersection.
- the length of AB.
Find the lengths of the medians of a ΔABC whose vertices are A(0,-1) , B(2,1) and C (0.3).
Find the coordinate of a point P which divides the line segment joining :
M( -4, -5) and N (3, 2) in the ratio 2 : 5.
Find the coordinate of a point P which divides the line segment joining :
D(-7, 9) and E( 15, -2) in the ratio 4:7.
Find the coordinates of point P which divides line segment joining A ( 3, -10) and B (3, 2) in such a way that PB: AB= 1.5.
The line joining P (-5, 6) and Q (3, 2) intersects the y-axis at R. PM and QN are perpendiculars from P and Q on the x-axis. Find the ratio PR: RQ.
Using section formula, show that the points A(7, −5), B(9, −3) and C(13, 1) are collinear
A line intersects y-axis and x-axis at point P and Q, respectively. If R(2, 5) is the mid-point of line segment PQ, them find the coordinates of P and Q.
