Advertisements
Advertisements
प्रश्न
The origin o (0, O), P (-6, 9) and Q (12, -3) are vertices of triangle OPQ. Point M divides OP in the ratio 1: 2 and point N divides OQ in the ratio 1: 2. Find the coordinates of points M and N. Also, show that 3MN = PQ.
उत्तर
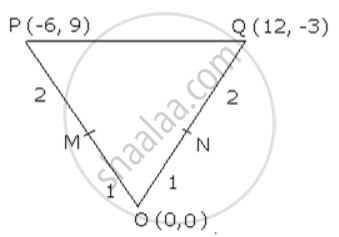
It is given that M divides OP in the ratio 1: 2 and point N divides OQ in the ratio 1: 2.
Using section formula, the coordinates of M are
`((-6 + 0)/ 3 , (9 + 0)/3) = (-2 , 3)`
Using section formula, the coordinates of N are
`((12 + 0)/3 , (-3 + 0)/3) = (4 , -1)`
Thus, the ooordinates of M and N are ( -2, 3) and ( 4, -1) respectively.
Now, using distance formula, we have:
PQ = `sqrt ((-6 -12)^2 + (9 + 3)^2) = sqrt (324 + 144) = sqrt 468`
MN = `sqrt ((4 + 2)^2 + (-1-3)^2) = sqrt (36 + 36) = sqrt 52`
It can be observed that :
PQ = `sqrt 468 = sqrt (9 xx 52) = 3 sqrt 52 = 3 "MN"`
Hence proved.
APPEARS IN
संबंधित प्रश्न
If the points A (6, 1), B (8, 2), C(9, 4) and D(p, 3) are vertices of a parallelogram, taken in order, find the value of p
If the coordinates of the mid points of the sides of a triangle are (1, 1), (2, – 3) and (3, 4) Find its centroid
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
In what ratio does the point `(24/11, y)` divide the line segment joining the points P(2, –2) and Q(3, 7)? Also find the value of y.
The mid-point of the segment AB, as shown in diagram, is C(4, –3). Write down the co-ordinates of A and B.
The mid point of the line segment joining (4a, 2b – 3) and (−4, 3b) is (2, –2a). Find the values of a and b.
Find the ratio in which the line segment joining A (2, -3) and B(S, 6) i~ divided by the x-axis.
Point P(5, –3) is one of the two points of trisection of the line segment joining the points A(7, –2) and B(1, –5).
Find the coordinates of the point R on the line segment joining the points P(–1, 3) and Q(2, 5) such that PR = `3/5` PQ.
If (2, 4) is the mid-point of the line segment joining (6, 3) and (a, 5), then the value of a is ______.
