Advertisements
Advertisements
प्रश्न
Q is a point on the line segment AB. The coordinates of A and B are (2, 7) and (7, 12) along the line AB so that AQ = 4BQ. Find the coordinates of Q.
उत्तर
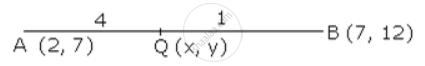
AQ : BQ = 4 : 1
Coordinates of Q are
Q (x , y) = Q `((4 xx 7 + 1xx 2)/(4 + 1) , (4 xx 12 + 1 xx 7)/(4 + 1))` = Q (6 , 11)
Thus the coordinates of Q are (6,11)
AQ = `sqrt ((2 - 6)^2 + (7 - 11)^2) = sqrt (16 + 16) = 4 sqrt 2`
BQ = `sqrt ((7 - 6)^2 + (12 - 11)^2) = sqrt (1 + 1) = sqrt 2`
⇒ AQ = 4 BQ
APPEARS IN
संबंधित प्रश्न
If A (5, –1), B(–3, –2) and C(–1, 8) are the vertices of triangle ABC, find the length of median through A and the coordinates of the centroid.
Two vertices of a triangle are (3, –5) and (–7, 4). If its centroid is (2, –1). Find the third vertex
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Show that the mid-point of the line segment joining the points (5, 7) and (3, 9) is also the mid-point of the line segment joining the points (8, 6) and (0, 10).
The line joining P(–4, 5) and Q(3, 2) intersects the y-axis at point R. PM and QN are perpendicular from P and Q on the x-axis Find:
- the ratio PR : RQ
- the coordinates of R.
- the area of the quadrilateral PMNQ.
- Write down the co-ordinates of the point P that divides the line joining A(−4, 1) and B(17, 10) in the ratio 1 : 2.
- Calculate the distance OP, where O is the origin.
- In what ratio does the y-axis divide the line AB?
Find the coordinate of a point P which divides the line segment joining :
A(-8, -5) and B (7, 10) in the ratio 2:3.
If the points A(1, 2), O(0, 0), C(a, b) are collinear, then ______.
If (a/3, 4) is the mid-point of the segment joining the points P(-6, 5) and R(-2, 3), then the value of ‘a’ is ______.
A line intersects y-axis and x-axis at point P and Q, respectively. If R(2, 5) is the mid-point of line segment PQ, them find the coordinates of P and Q.
