Advertisements
Advertisements
प्रश्न
Q is a point on the line segment AB. The coordinates of A and B are (2, 7) and (7, 12) along the line AB so that AQ = 4BQ. Find the coordinates of Q.
उत्तर
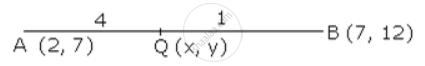
AQ : BQ = 4 : 1
Coordinates of Q are
Q (x , y) = Q `((4 xx 7 + 1xx 2)/(4 + 1) , (4 xx 12 + 1 xx 7)/(4 + 1))` = Q (6 , 11)
Thus the coordinates of Q are (6,11)
AQ = `sqrt ((2 - 6)^2 + (7 - 11)^2) = sqrt (16 + 16) = 4 sqrt 2`
BQ = `sqrt ((7 - 6)^2 + (12 - 11)^2) = sqrt (1 + 1) = sqrt 2`
⇒ AQ = 4 BQ
APPEARS IN
संबंधित प्रश्न
Find the coordinates of the point which divides the line segment joining the points (6, 3) and (– 4, 5) in the ratio 3 : 2 internally.
If the coordinates of the mid points of the sides of a triangle are (1, 1), (2, – 3) and (3, 4) Find its centroid
If A and B are (−2, −2) and (2, −4), respectively, find the coordinates of P such that `"AP" = 3/7 "AB"` and P lies on the line segment AB.
Calculate the ratio in which the line joining the points (–3, –1) and (5, 7) is divided by the line x = 2. Also, find the co-ordinates of the point of intersection.
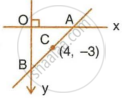
The mid-point of the segment AB, as shown in diagram, is C(4, –3). Write down the co-ordinates of A and B.
The mid point of the line segment joining (4a, 2b – 3) and (−4, 3b) is (2, –2a). Find the values of a and b.
Find the coordinates of a point P, which lies on the line segment joining the points A (−2, −2), and B (2, −4), such that `AP=3/7 AB`.
If the points A(1, 2), O(0, 0), C(a, b) are collinear, then ______.
The point which divides the line segment joining the points (7, –6) and (3, 4) in ratio 1 : 2 internally lies in the ______.
The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC. Find the coordinates of points Q and R on medians BE and CF, respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1
