Advertisements
Advertisements
प्रश्न
The line joining P(–4, 5) and Q(3, 2) intersects the y-axis at point R. PM and QN are perpendicular from P and Q on the x-axis Find:
- the ratio PR : RQ
- the coordinates of R.
- the area of the quadrilateral PMNQ.
उत्तर
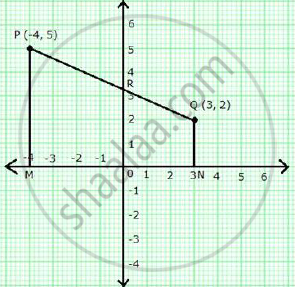
i. Let point R (0, y) divides PQ in the ratio k : 1.
We have:
`x = (k xx 3 + 1 xx (-4))/(k + 1)`
`0 = (3k - 4)/(k + 1)`
`0 = 3k - 4`
`k = 4/3`
Thus, PR : RQ = 4 : 3
ii. Also, we have:
`y = (k xx 2 + 1 xx 5)/(k + 1)`
`y = (2k + 5)/(k + 1)`
`y = (2 xx 4/3 + 5)/(4/3 + 1)`
`y = (8 + 15)/(4 + 3)`
`y = 23/7`
Thus, the co-ordinates of point R are `(0, 23/7)`
iii. Area of quadrilateral PMNQ
= `1/2 xx (PM + QN) xx MN`
= `1/2 xx (5 + 2) xx 7`
= `1/2 xx 7 xx 7`
= 24.5 sq. units
APPEARS IN
संबंधित प्रश्न
The three vertices of a parallelogram taken in order are (–1, 0), (3, 1) and (2, 2) respectively. Find the coordinates of the fourth vertex.
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Points A, B, C and D divide the line segment joining the point (5, –10) and the origin in five equal parts. Find the co-ordinates of B and D.
P is a point on the line joining A(4, 3) and B(–2, 6) such that 5AP = 2BP. Find the co-ordinates of P.
AB is a diameter of a circle with centre C = (–2, 5). If A = (3, –7), find
- the length of radius AC.
- the coordinates of B.
Find the ratio in which the line y = -1 divides the line segment joining (6, 5) and (-2, -11). Find the coordinates of the point of intersection.
In the figure given below, the line segment AB meets X-axis at A and Y-axis at B. The point P (- 3, 4) on AB divides it in the ratio 2 : 3. Find the coordinates of A and B.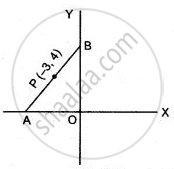
The line segment joining the points A(3, 2) and B(5, 1) is divided at the point P in the ratio 1 : 2 and it lies on the line 3x – 18y + k = 0. Find the value of k.
The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC. What are the coordinates of the centroid of the triangle ABC?
A line intersects y-axis and x-axis at point P and Q, respectively. If R(2, 5) is the mid-point of line segment PQ, them find the coordinates of P and Q.
