Advertisements
Advertisements
प्रश्न
In the figure given below, the line segment AB meets X-axis at A and Y-axis at B. The point P (- 3, 4) on AB divides it in the ratio 2 : 3. Find the coordinates of A and B.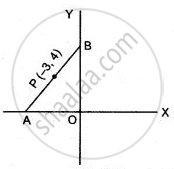
उत्तर
AP : PB = 2 : 3
Let A(x, 0) and B(0, y)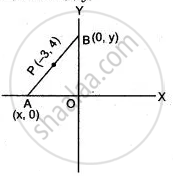
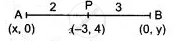
∴ By section formula
`(2 xx 0 + 3 xx x)/(2 + 3)` = -3
⇒ 3x = -15
x = -5
and `(2 xx y + 3 xx 0)/(2 + 3)` = 4
⇒ 2y = 20
⇒ y = 10
∴ Coordinates of A = (x, 0) = (-5, 0)
and B = (0, y) = (0, 10).
APPEARS IN
संबंधित प्रश्न
Find the ratio in which y-axis divides the line segment joining the points A(5, –6) and B(–1, –4). Also find the coordinates of the point of division.
If the coordinates of the mid points of the sides of a triangle are (1, 1), (2, – 3) and (3, 4) Find its centroid
Find the ratio in which the line segment joining the points (-3, 10) and (6, -8) is divided by (-1, 6).
Find the ratio in which P(4, m) divides the line segment joining the points A(2, 3) and B(6, –3). Hence find m.
Show that the lines x = O and y = O trisect the line segment formed by joining the points (-10, -4) and (5, 8). Find the points of trisection.
Find the ratio in which the point R ( 1, 5) divides the line segment joining the points S (-2, -1) and T (5, 13).
Point P(– 4, 6) divides point A(– 6, 10) and B(m, n) in the ratio 2:1, then find the coordinates of point B
The point which divides the line segment joining the points (7, –6) and (3, 4) in ratio 1 : 2 internally lies in the ______.
If P(9a – 2, – b) divides line segment joining A(3a + 1, –3) and B(8a, 5) in the ratio 3 : 1, find the values of a and b.
The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC. Find the coordinates of the point P on AD such that AP : PD = 2 : 1
