Advertisements
Advertisements
प्रश्न
In the adjoining figure, write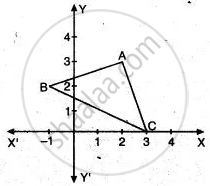
(i) The coordinates of A, B and C.
(ii) The equation of the line through A and | | to BC.
उत्तर
(i) A = (2, 3), B = (-1, 2), C = (3, 0).
(ii) Slope of BC = `(y_2 - y_1)/(x_2 - x_1) = (2 - 0)/(-1 - 3) = (2)/(-4)`
m1 = `(-1)/(2)`
Since lines are parallel
∴ m1 = m2
Hence, m2 = `-(1)/(2)`
and passing through point (2, 3)
∵ Equation of line is y - y1 = m2 (x - x1)
∴ required line is y - 3 = `(-1)/(2)(x - 2)`
2y - 6 = -x + 2
x + 2y = 8.
APPEARS IN
संबंधित प्रश्न
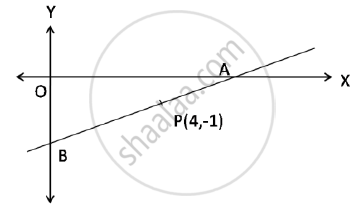
A line AB meets X – axis at A and Y –axis at B. P (4, -1) divides AB in the ratio 1 : 2.
1) Find the coordinates of A and B.
2) Find the equation of the line through P and perpendicular to AB.
Find the equation of a line whose : y-intercept = 2 and slope = 3
Find the equation of the line whose slope is `-4/3` and which passes through (−3, 4).
Find the equation of the line passing through : (−1, −4) and (3, 0)
The co-ordinates of two points P and Q are (2, 6) and (−3, 5) respectively. Find:
- the gradient of PQ;
- the equation of PQ;
- the co-ordinates of the point where PQ intersects the x-axis.
In triangle ABC, the co-ordinates of vertices A, B and C are (4, 7), (–2, 3) and (0, 1) respectively. Find the equation of median through vertex A. Also, find the equation of the line through vertex B and parallel to AC.
Find the value of m if the line 2x + 5y + 12 = 0 passes through the point
( 4,m ).
The line 4x + 3y = 11 bisects the join of ( 6,m) and (p,9). Find the value of m.
If the image of the point (2,1) with respect to the line mirror be (5, 2). Find the equation of the mirror.
In the given diagram, OA = OB, ∠OAB = 𝜃 and the line AB passes through point P (-3, 4).
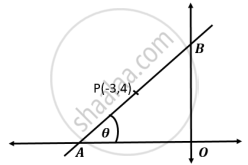
Find:
- Slope and inclination (𝜃) of the line AB
- Equation of the line AB
