Advertisements
Advertisements
प्रश्न
The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC. Find the coordinates of the point P on AD such that AP : PD = 2 : 1
उत्तर
According to the question,
The vertices of ΔABC = A, B and C
Coordinates of A, B and C = A(x1, y1), B(x2, y2), C(x3, y3)
Let the coordinates of a point P be (x, y)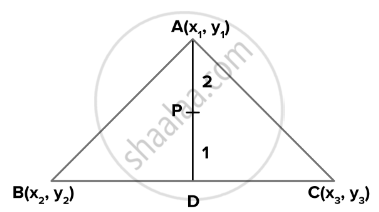
Given,
The ratio in which the point P(x, y), divide the line joining,
`"A"(x_1, y_1)` and `"D"((x_2 + x_3)/2, (y_2 + y_3)/2)` = 2 : 1
Then,
Coordinates of P = `[(2 xx ((x_2 + x_3)/2) + 1 xx x_1)/(2 + 1), (2 xx ((y_2 + y_3)/2) + 1 xx y_1)/(2 + 1)]`
By using internal section formula;
= `((m_1x_2 + m_2x_1)/(m_1 + m_2), (m_1y_2 + m_2y_1)/(m_1 + m_2))`
= `((x_2 + x_3 + x_1)/3, (y_2 + y_3 + y_1)/3)`
APPEARS IN
संबंधित प्रश्न
Let P and Q be the points of trisection of the line segment joining the points A(2, -2) and B(-7, 4) such that P is nearer to A. Find the coordinates of P and Q.
In what ratio does the x-axis divide the line segment joining the points (2, –3) and (5, 6)? Also, find the coordinates of the point of intersection.
Find the coordinates of a point A, where AB is the diameter of circle whose centre is (2, -3) and B is (1, 4).
Find the coordinates of the points which divide the line segment joining A (−2, 2) and B (2, 8) into four equal parts.
Find the lengths of the medians of a triangle whose vertices are A (−1,3), B(1,−1) and C(5, 1).
If the points (-2, -1), (1, 0), (x, 3) and (1, y) form a parallelogram, find the values of x and y.
Find the coordinate of a point P which divides the line segment joining :
M( -4, -5) and N (3, 2) in the ratio 2 : 5.
In what ratio is the line joining (2, -4) and (-3, 6) divided by the line y = O ?
Find the ratio in which the line y = -1 divides the line segment joining (6, 5) and (-2, -11). Find the coordinates of the point of intersection.
Find the points of trisection of the segment joining A ( -3, 7) and B (3, -2).
