Advertisements
Advertisements
प्रश्न
In what ratio is the line joining (2, -4) and (-3, 6) divided by the line y = O ?
उत्तर
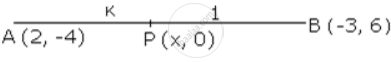
Let P (x, O) be tne point on line y = 0 i.e. x-axis which divides the line segment AB in the ratio k : 1.
Coordinates of P are
x = `(3 "k" + 2)/("k + 1")` , 0 = `(6"k" - 4)/("k + 1")`
⇒ 6k = 4
⇒ k = `2/3`
Hence tne required ratio is 2: 3.
APPEARS IN
संबंधित प्रश्न
In what ratio does the x-axis divide the line segment joining the points (2, –3) and (5, 6)? Also, find the coordinates of the point of intersection.
Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).
Find the ratio in which P(4, m) divides the line segment joining the points A(2, 3) and B(6, –3). Hence find m.
Show that the mid-point of the line segment joining the points (5, 7) and (3, 9) is also the mid-point of the line segment joining the points (8, 6) and (0, 10).
If A = (−4, 3) and B = (8, −6)
- Find the length of AB.
- In what ratio is the line joining A and B, divided by the x-axis?
The line segment joining A(4, 7) and B(−6, −2) is intercepted by the y – axis at the point K. write down the abscissa of the point K. hence, find the ratio in which K divides AB. Also, find the co-ordinates of the point K.
Find the co-ordinates of the centroid of a triangle ABC whose vertices are: A(–1, 3), B(1, –1) and C(5, 1).
Find the coordinate of a point P which divides the line segment joining :
A (3, -3) and B (6, 9) in the ratio 1 :2.
A (30, 20) and B ( 6, -4) are two fixed points. Find the coordinates of a point Pin AB such that 2PB = AP. Also, find the coordinates of some other point Qin AB such that AB = 6 AQ.
The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC. The median from A meets BC at D. Find the coordinates of the point D.
