Advertisements
Advertisements
प्रश्न
In what ratio is the line joining (2, -4) and (-3, 6) divided by the line y = O ?
उत्तर
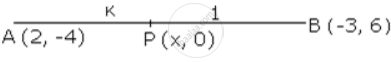
Let P (x, O) be tne point on line y = 0 i.e. x-axis which divides the line segment AB in the ratio k : 1.
Coordinates of P are
x = `(3 "k" + 2)/("k + 1")` , 0 = `(6"k" - 4)/("k + 1")`
⇒ 6k = 4
⇒ k = `2/3`
Hence tne required ratio is 2: 3.
APPEARS IN
संबंधित प्रश्न
The three vertices of a parallelogram taken in order are (–1, 0), (3, 1) and (2, 2) respectively. Find the coordinates of the fourth vertex.
Find the ratio in which the line segment joining A (1, −5) and B (−4, 5) is divided by the x-axis. Also, find the coordinates of the point of division.
Calculate the ratio in which the line joining the points (–3, –1) and (5, 7) is divided by the line x = 2. Also, find the co-ordinates of the point of intersection.
The line segment joining A (2, 3) and B (6, –5) is intercepted by x-axis at the point K. Write down the ordinate of the point K. Hence, find the ratio in which K divides AB. Also, find the coordinates of the point K.
In the given figure, line APB meets the x-axis at point A and y-axis at point B. P is the point (−4, 2) and AP : PB = 1 : 2. Find the co-ordinates of A and B.
A(20, 0) and B(10, –20) are two fixed points. Find the co-ordinates of the point P in AB such that : 3PB = AB. Also, find the co-ordinates of some other point Q in AB such that : AB = 6 AQ.
Find the coordinates of a point P, which lies on the line segment joining the points A (−2, −2), and B (2, −4), such that `AP=3/7 AB`.
Find the coordinate of a point P which divides the line segment joining :
5(2, 6) and R(9, -8) in the ratio 3: 4.
In what ratio does the point (1, a) divided the join of (−1, 4) and (4, −1) Also, find the value of a.
Find the ratio in which the line segment joining P ( 4, -6) and Q ( -3, 8) is divided by the line y = 0.
