Advertisements
Advertisements
प्रश्न
Find the ratio in which the line segment joining A (1, −5) and B (−4, 5) is divided by the x-axis. Also, find the coordinates of the point of division.
उत्तर
Let the ratio in which the line segment joining A (1, −5) and B (−4, 5) is divided by x-axis be K : 1
Therefore, the coordinates of the point of division is
x = `(m_1x_2 + m_2x_1)/(m_1 + m_2), 0 = (m_1y_2 + m_2y_1)/(m_1 + m_2)`
x = `(k (-4) + 1 (1))/(k + 1), 0 = (k (5)+ 1 (-5))/(k + 1)`
x = `(-4k+1)/(k+1), 0 = (5k-5)/(k+1)`
x (k + 1) = -4 + 1 and 5k - 5 = 0
k = 1 Now, x (k + 1) = -4 + 1
⇒ x (1 + 1) = -4 + 1
⇒ 2x = -3
⇒ x = `-3/2`
∴ The required ratio is k:1 = 1:1
Coordinates of P are (x, 0) = `(-3/2,0)`
APPEARS IN
संबंधित प्रश्न
Let P and Q be the points of trisection of the line segment joining the points A(2, -2) and B(-7, 4) such that P is nearer to A. Find the coordinates of P and Q.
If the points A (6, 1), B (8, 2), C(9, 4) and D(p, 3) are vertices of a parallelogram, taken in order, find the value of p
If A(–2, –1), B(a, 0), C(4, b) and D(1, 2) are the vertices of a parallelogram, find the values of a and b
If the coordinates of the mid points of the sides of a triangle are (1, 1), (2, – 3) and (3, 4) Find its centroid
Find the ratio in which P(4, m) divides the line segment joining the points A(2, 3) and B(6, –3). Hence find m.
Find the ratio in which the join of (–4, 7) and (3, 0) is divided by the y-axis. Also, find the co-ordinates of the point of intersection.
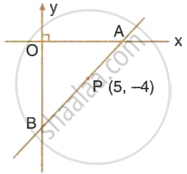
The point P (5, – 4) divides the line segment AB, as shown in the figure, in the ratio 2 : 5. Find the co-ordinates of points A and B. Given AP is smaller than BP.
A (–3, 4), B (3, –1) and C (–2, 4) are the vertices of a triangle ABC. Find the length of line segment AP, where point P lies inside BC, such that BP : PC = 2 : 3.
In what ratio is the line joining A(0, 3) and B(4, –1) divided by the x-axis? Write the co-ordinates of the point where AB intersects the x-axis.
- Write down the co-ordinates of the point P that divides the line joining A(−4, 1) and B(17, 10) in the ratio 1 : 2.
- Calculate the distance OP, where O is the origin.
- In what ratio does the y-axis divide the line AB?
Find the coordinate of a point P which divides the line segment joining :
A (3, -3) and B (6, 9) in the ratio 1 :2.
Find the coordinate of a point P which divides the line segment joining :
5(2, 6) and R(9, -8) in the ratio 3: 4.
Find the coordinates of the points of trisection of the line segment joining the points (3, -3) and ( 6, 9).
Point P(– 4, 6) divides point A(– 6, 10) and B(m, n) in the ratio 2:1, then find the coordinates of point B
If (a/3, 4) is the mid-point of the segment joining the points P(-6, 5) and R(-2, 3), then the value of ‘a’ is ______.
The fourth vertex D of a parallelogram ABCD, whose three vertices are A(–2, 3), B(6, 7) and C(8, 3), is ______.
Find the ratio in which the point `P(3/4, 5/12)` divides the line segment joining the points `A(1/2, 3/2)` and B(2, –5).
If (2, 4) is the mid-point of the line segment joining (6, 3) and (a, 5), then the value of a is ______.
What is the ratio in which the line segment joining (2, -3) and (5, 6) is divided by x-axis?
