Advertisements
Advertisements
प्रश्न
Find the ratio in which P(4, m) divides the line segment joining the points A(2, 3) and B(6, –3). Hence find m.
उत्तर
Let P divides AB in a ratio of λ : 1
Therefore, coordinates of the point P are `((6lambda+2)/(lambda + 1), (-3lambda + 3)/(lambda + 1))`
Given that coordinates of the point P are (4, m).
`=> (6lambda + 2)/(lambda + 1) = 4`
`=> 6lambda + 2 = 4lambda + 4`
`=> lambda = 1`
Hence, the point P divides AB in a ratio of 1 : 1.
Replacing the value of λ = 1 in y-coordinate of P, we get
`(-3(1)+3)/(1+1) = m`
`=> m = 0`
Thus, y-coordinate of P is equal to 0.
APPEARS IN
संबंधित प्रश्न
If A(–2, –1), B(a, 0), C(4, b) and D(1, 2) are the vertices of a parallelogram, find the values of a and b
P is a point on the line joining A(4, 3) and B(–2, 6) such that 5AP = 2BP. Find the co-ordinates of P.
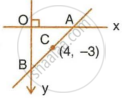
The mid-point of the segment AB, as shown in diagram, is C(4, –3). Write down the co-ordinates of A and B.
B is a point on the line segment AC. The coordinates of A and B are (2, 5) and (1, 0). If AC= 3 AB, find the coordinates of C.
The origin o (0, O), P (-6, 9) and Q (12, -3) are vertices of triangle OPQ. Point M divides OP in the ratio 1: 2 and point N divides OQ in the ratio 1: 2. Find the coordinates of points M and N. Also, show that 3MN = PQ.
Find the ratio in which the point R ( 1, 5) divides the line segment joining the points S (-2, -1) and T (5, 13).
If (a/3, 4) is the mid-point of the segment joining the points P(-6, 5) and R(-2, 3), then the value of ‘a’ is ______.
Find the ratio in which the line 2x + 3y – 5 = 0 divides the line segment joining the points (8, –9) and (2, 1). Also find the coordinates of the point of division.
The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC. Find the coordinates of points Q and R on medians BE and CF, respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1
If (2, 4) is the mid-point of the line segment joining (6, 3) and (a, 5), then the value of a is ______.
